Skrivning i matematik - Matematik - GRUNDSKOLE

I matematik skal eleverne lære, at symboler og tegn repræsenterer noget. Det kan være en mængde, en regneoperation, et forhold eller en relation. Et symbol i matematik dækker altså over et helt ord eller et omfattende taleudtryk.

For eleverne vil matematiksproget være et sprog af 2. orden, som skal kobles med deres sprog af 1. orden, nemlig hverdagssproget. Det er centralt, at matematiklæreren hele tiden søger at skabe forbindelse mellem elevernes hverdagssprog og det matematiske sprog i klasserummet, så eleverne oplever at lytte til sproget samt at læse, skrive og samtale om sprogets symboler og tegn

Første trinforløb

I første trinforløb møder eleverne en række tal og symboler, som de gradvist skal blive fortrolige med. Der bør løbende foregå en mundtlig og en skriftlig bearbejdning af tal og symboler med brug af repræsentationer og konkrete materialer. Eleverne møder i dette trinforløb regnehistorier, der udtrykker små situationer fra hverdagen, som kan løses ved hjælp af matematik. Første udfordring kan være, at eleverne overhovedet lærer at identificere en regnehistorie. Eleverne skal på sigt kunne omsætte regnehistorier til regneudtryk og gå fra hverdagssprog til matematiksprog. Her er direkte arbejde med koblingen mellem sprog af 1. orden og sprog af 2. orden i spil. Nogle elever kan have glæde af at bruge lommeregner eller en simpel CAS-lommeregner.

Eksempel: Eleverne skal oversætte: Peter har 45 kr. Han vil købe en gave til sin mor, som koster 79 kr. Hvor mange penge mangler Peter?

Regnehistorien kan oversættes til: "Hvad skal jeg plusse 45 med for at få 79?" Den kan også tegnes som 45 + = 79, og der kunne skrives 45 + mangler = 79 eller 45 + m = 79. Andre vil kunne skrive 79 – 45, men da eleverne ikke nødvendigvis ser denne situation som en subtraktionskontekst, vil det være en fin støtte at arbejde med simpel algebra, ikke som formel ligningsløsning, men som understøttelse af tænkningen.

Eleverne kan tegne deres egne symboler for det tal, de skal finde. Det er matematisk skrivning med symbolholdige udtryk, og symbolerne kan være andet end tal og regnetegn. Symbolerne kan være med til at repræsentere elevernes tænkning.

Andet trinforløb

I andet trinforløb er det naturligt at udvikle og udvide elevernes tekstbegreb i matematik. . Begrebet dækker over alt fra grafer, diagrammer, tegninger, matematisk symbolsprog, faktabokse til sammenhængende tekst. Eleverne skal både lære at læse, tolke/samtale om og selv udtrykke sig gennem de forskellige tekster, faget rummer. Det er væsentligt at bruge tid på de forskellige teksttyper og omtale dem som matematikholdige tekster, så eleverne tidligt lærer at tillægge disse teksttyper værdi. Her er den faglige skrivning i de forskellige teksttyper central. Dermed er det at udtrykke sig gennem grafer, symbolholdige udtryk, diagrammer og tabeller altså at betragte som skrivning i matematik.

Eksempel: Opgave: Vis selv resultatet af din undersøgelse i et diagram. Hvilket diagram er det bedste?

For at forstå forskellen på forskellige diagrammers virkemåde, er eleverne nødt til at fremstille diagrammer og undersøge: Hvad kan et cirkeldiagram i forhold til et søjlediagram og omvendt? Kun ved selv at skrive, kan eleverne få deres eget sprog om, hvordan diagrammerne virker, hvordan de kommunikerer et datasæt, og hvad der kan tolkes af diagrammerne.

Begrebet tekstopgaver folder sig for alvor ud i løbet af andet trinforløb, og eleverne skal lære at trække de relevante informationer ud af teksten, omsætte dem til et matematisk problem, som de skal løse, og kommunikere et svar.

Symboler, begreber og definitioner

I arbejdet med symbolholdige udtryk er det en god idé i både andet og tredje trinforløb at have fokus på symbolernes betydning, da flere symboler kan have flere betydninger. Bogstavers rolle kan eksempelvis variere i symbolholdige udtryk lige fra at være pladsholder for et bestemt tal, som det ses i en ligning, 2x + 3 = 5, til at være en variabel, der kan antage forskellige værdier som i udtrykket 2a+3, til at være et symbol for et bestemt tal, som det ses i brugen af π.

På samme måde har lighedstegnet vidt forskellige roller. Når eleverne bruger eksempelvis CAS-værktøjer til symbolholdige udtryk, vil de i flere situationer skulle vælge mellem forskellige lighedstegn, alt efter om de beregner, løser en ligning eller tildeler en værdi. Skrivning i matematik betyder altså nogle gange, at eleverne skal dvæle ved de enkelte symbolers betydning og udforske betydningen i deres skrivning.

Eksempel: Skriv et regneudtryk, som viser omkredsen af et rektangel, hvor længden er det dobbelte af bredden. Dit regneudtryk skal passe på alle rektangler, hvor længden er det dobbelt af bredden.

Eleverne kunne skrive: O=2b+b+2b+b eller O=6b. Hvis de antager, at bredden kaldes b. Der er mange mellemsvar, og nogle elever kan have brug for at starte med konkrete tal, for gradvist at arbejde med det algebraiske sprog. Der kan være gode samtaler på klassen om, hvad O og b betyder i regneudtrykket, og hvorfor de to eksempler oven for begge kan bruges og giver det samme: Hvad betyder lighedstegnet i regneudtrykket? Skal man regne noget ud mon? Hvad kan man regne ud?

Begreber og definitioner

I løbet af andet og tredje trinforløb vil elevernes begrebsverden i matematik blive udvidet i takt med, at de hele tiden møder nye områder af matematikken eller bygger oven på tidligere områder. Ved nye begreber skal eleverne møde mange repræsentationer for begreberne og få en masse erfaringer med de konkrete begreber. For at give et øjebliksbillede af elevernes tænkning om et begreb, kan der arbejdes med et begrebskort eller med at skrive egentlige definitioner på begreberne, hvilket kan indfange elevernes viden og forståelse.

At arbejde med egne begrebsdefinitioner kan være med til at udvikle elevernes indre stemme, deres sprog af 1. orden, så de får en klar bevidsthed om, hvordan de selv tænker om begreberne. Det kan være frugtbart at lade eleverne møde hinandens begrebsdefinitioner, og det leder frem mod, at eleverne på sigt kan møde de matematiske definitioner, der findes til mange begreber i faget. Sigtet er ikke at ensrette elevernes egne definitioner, men at få dem i spil og udfordret i undervisningen. Det kan betragtes som et lille pitstop, hvor eleverne skal samle tankerne og forsøge at strukturere dem mundtligt og skriftligt.

Tredje trinforløb

I dette trinforløb fylder arbejdet med faglig skrivning gradvist mere, da elevernes skrivning i matematik efterhånden kan og bør antage mange forskellige udtryk. Eleverne skal udvikle gode strategier for at angribe tekstopgaver eller skriftlige problemer, når de møder dem i matematik, for eksempel kan eleverne blive opmærksomme på signalord. Det er ord, som sender signaler om, hvilke former for svar, der forventes, eller hvad der skal til at for at løse opgaven. Signalord kan være:

Beregn - kalder typisk på en beregning, hvor der fremgår et eller andet regneudtryk.
Forklar - kalder på en skriftlig forklaring, som kan bygge på beregninger, tegninger, hvor der begrundes med noget matematik.
Undersøg - fortæller, at der muligvis ikke er en bestemt metode, som skal bruges, men at eleverne kan vælge mange forskellige metoder og på en eller anden måde dokumentere deres fremgangsmåde og resultat. Ofte vil der være brug for en form for konklusion på undersøgelsen.

Det kan være en fordel, hvis eleverne prøver både at arbejde med at lave gode svar på opgaver, der bruger bestemte signalord, og at eleverne finder på opgaver til hinanden, hvor de bruger bestemte signalord.

Eksempel: Hvis I har en figurfølge som herunder, hvilke opgaver kan I så stille til hinanden med følgende signalord: Hvor stort er? Beregn? Forklar? Undersøg?

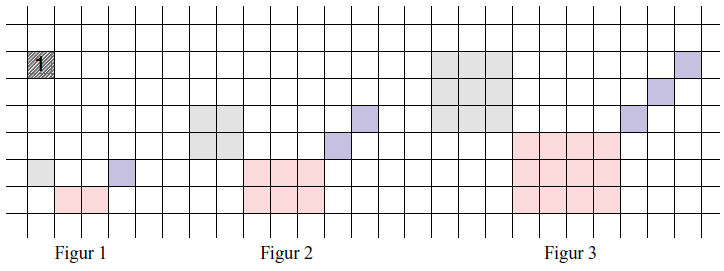
Hvis eleverne udarbejder deres egne facitlister, kan der ligge mange frugtbare diskussioner i, at de prøver at løse hinandens opgaver og diskutere facitlister. Arbejdet med både selv at løse og skrive opgaver med signalord, kan give en god dybdeforståelse af, hvilke typer svar, de forskellige måder at spørge på i matematikopgaver, kalder på.

Prøverne i matematik

Arbejdet med de forskellige teksttyper i matematik strækker sig også over tredje trinforløb, hvor elevernes kommunikation gradvist nuanceres og tilpasses en modtagerbevidsthed. Eleverne skal blandt andet kunne tilpasse deres kommunikationsform og faglige præcision, så den harmonerer med modtageren, situationen og kommunikationens formål. Trinforløbet arbejder sig hen mod de skriftlige prøver, som kan betragtes som en særlig genre i matematikfaget.

Prøverne rummer en række tekstopgaver, hvor eleverne selv skal trække relevante informationer ud af teksten, løse problemet samt kommunikere skriftligt om, hvordan de er kommet frem til en løsning, ofte med begrundelser og ræsonnementer i spil. Den faglige skrivning knytter således an til arbejdet med de matematiske kompetencer, da flere elementer fra en del af kompetencerne ofte er i spil, når eleverne skriver tekster i matematik.

Kriterier for skrivning

Klassen kan i fællesskab udvikle gode kriterier for skrivning i matematik. Eleverne kan blive klogere på deres egen kommunikation ved at spejle sig i andres produkter, eller ved at læreren anvender såkaldte modeltekster, som er eksempler udarbejdet af enten andre elever eller af læreren selv. Eleverne kan helt lavpraktisk sortere de forskellige eksempler på besvarelser ud fra, hvor godt de er kommunikeret, og ikke om de er regnet rigtigt eller forkert. På baggrund af sorteringerne kan eleverne være med til at opstille kriterier for god kommunikation, som de bagefter aktivt kan bruge i deres egen skrivning

Et lignende arbejde kan i princippet udføres for enhver teksttype, og læreren kan producere eksempler på relevante teksttyper, som er mere eller mindre hensigtsmæssige, så eleverne kan få blik for disse hensigtsmæssig- og uhensigtsmæssigheder og bruge dem aktivt i deres egen skrivning. Det kan være i forhold til grafer - hvor man tager et uhensigtsmæssigt udklip af koordinatsystemet, eller hvor forholdet mellem x- og y-akse ikke er hensigtsmæssigt for det grafiske billede.

For nogle elever kan det være en udfordring at få hul på at skrive ræsonnementer eller forklaringer. Disse elever kan bruge sætningsstartere som:

Min beregning viste, at …
Jeg tror, at det er…, fordi…
Min undersøgelse viser, at …
Det kan ikke passe, fordi…
Diagrammet viser, at …
Først gjorde jeg…, så …

Et arbejde med skriftlighed i ræsonnementer bør altid følges af en mundtlighed. Klassen kan starte mundtligt og fælles, eller eleverne kan starte med en læringsmakker, så de får gang i en stemme, der kan blive til en indre stemme, når de skal skriftliggøre deres ræsonnementer.

Matematikvejlederens og fagteamets rolle

Matematikvejlederen kan understøtte arbejdet med faglig skrivning ved at sætte fokus på det som en indsats i den daglige undervisning som et perspektiv på ethvert undervisningsforløb. Der kan tages udgangspunkt i spørgsmål som:

Hvordan får vi løbende skabt kobling mellem elevernes begrebsbilleder og deres begrebsforståelse?
Hvordan får vi forbundet elevernes hverdagssprog med matematikkens fagsprog?
Hvilken skrivedel er der i undervisningsforløbet?
Hvilke teksttyper er i spil?
Hvordan får vi eleverne til selv at skulle skrive i den specifikke teksttype?

Fagteamet kan videndele og bistå hinanden i at indsamle en teksttypebank, som kan bidrage til at udvikle elevernes fornemmelse af de forskellige teksttyper. Den kan indeholde autentiske grafer fra aviser eller eksempler på elevprodukter.

Der kan ligge en frugtbar diskussion i at få vendt og udfoldet teksttypebegrebet i matematik:

Hvad er egentlig en matematikholdig tekst? Hvad kendetegner den?
Hvordan får vi eleverne til at skrive den slags tekster selv?
Hvor passer det naturligt ind i vores undervisning?

Der er ikke noget i vejen for at lave fordybelsesindsatser omkring faglig læsning og skrivning i matematik, men det er helt centralt, at det finder vej til den daglige undervisning i små bidder, som en løbende og naturlig del af den måde, hvorpå eleverne kommunikerer i, med og om matematik.

Inspiration

Artikel om sproglig udvikling: Sproglig udvikling i matematik

Artikel om læsning i faget: Læsning i matematik

Læs også om arbejdet med sproglig udvikling i faghæftet for matematik, som findes her: Læseplan og vejledning

Du finder afsnittet om det tværgående tema sproglig udvikling på side 109-111.

Kreditering

Artiklen er udarbejdet af Rikke Teglskov, Pædagogisk konsulent, UCL.