Sæt fokus på regnestrategier, og lær eleverne at tænke fleksibelt

Elever i matematikvanskeligheder er kendetegnet ved at hænge fast i rigide og primitive tællestrategier op gennem hele skoleforløbet. Det kan komme til udtryk ved, at disse elever ikke har andre strategier end at tælle sig frem, hver gang de møder et regnestykke, de endnu ikke kan udenad. Det ser ud til at kunne forhindre et optimalt udviklingsforløb i matematik, hvis eleverne kun har få og uhensigtsmæssige strategier. Derfor er undervisning i regnestrategier noget, der bør arbejdes målrettet med allerede fra starten af skoleforløbet.

Strategier og metoder

En vigtig opmærksomhed er, at regnestrategier og regnemetoder ikke er det samme:

• Regnemetoder betegner en systematisk fremgangsmåde, altså den ramme eleven vælger at støtte sig til under udregningen. Hvis eleven tæller sig frem, kan en metode være at støtte sig til fingrene eller en talplade. Senere kan metoden være elevernes måde at skrive ned og holder styr på, hvor de er kommet til i regnestykket. 
• Regnestrategier omfatter en mere overordnet tilgang til et regnestykke, hvor eleven vælger en strategi, som egner sig godt til tallene i regnestykket.

I læseplanen for matematik står der: ”Det er centralt, at læreren udfordrer og støtter de enkelte elever på en måde, så eleverne udvikler deres regnestrategier på baggrund af deres talforståelse frem for at lære procedurer for opstilling og udregning. Der sigtes ikke mod opøvelsen af standardiserede algoritmer”. I stedet for at lære de gamle algoritmer, skal fokus i undervisningen være på elevernes udvikling af regnestrategier og talforståelse. Når eleverne har behov for en regnemetode at støtte sig til, er det derfor vigtigt, at metoden giver plads til forskellige mellemregninger, så det er elevernes forståelse og regnestrategier, som styrer og udfylder metoden – og ikke metoden som styrer eleverne.

Tællestrategier og hukommelsesstrategier

Regnestrategier opdeles i tællestrategier og hukommelsesstrategier.

Tællestrategier
Tællestrategier er et helt naturligt sted at starte. Det er en form for grundlæggende forståelse af regningsarterne, hvor eleverne tæller sig frem til resultatet. Til regnestykket 3+4 kan en tællestrategi være, at eleverne først finder tre fingre frem og så fire mere, for til sidst at tælle dem alle sammen og finde ud af, at der er syv i alt.

En videreudviklet tællestrategi er, at eleverne starter på det ene tal og tæller videre. Tællestrategier er backupstrategier, som er gode at kunne falde tilbage på. Det er sikkert og stabilt at tælle sig frem, men det er også langsomt og ressourcekrævende, så elever, der tæller meget, bruger flere kræfter og bliver hurtigere trætte.

Hukommelsesstrategier
Hukommelsesstrategier er strategier, hvor eleverne løser opgaven ved at benytte viden, de har lagret i hukommelsen. Til regnestykket 3+4 kan eleverne tænke: “Jeg ved ikke, hvad 3+4 er, men jeg ved, at 3+3=6, og så må 3+4 være én mere, altså 7”. Eleverne trækker altså på viden fra deres hukommelse og udnytter denne viden i opgaveløsningen.

Hukommelsesstrategierne er retrievalstrategier, og de er mere effektive og langt mindre ressourcekrævende for eleverne end tællestrategierne.

Eleverne skal gå fra at tælle til at tænke
Selvom det er helt naturligt, at eleverne tæller meget i de første skoleår, så er det vigtigt, at de oplever en fleksibel tilgang til regning og allerede på de yngste klassetrin får mulighed for, at udvikle deres regnestrategier til små tal, da vedvarende brug af tællestrategier risikerer at fastlåse eleverne i deres strategibrug. En optimal udvikling af strategier til hovedregning går fra tællestrategier mod gradvist øget brug af hukommelsesstrategier, men mange elever opdager eller udvikler ikke hensigtsmæssige hukommelsesstrategier af sig selv.

Man kunne måske tro, at eleverne holder op med at tælle, hvis bare de får regnestykker nok, men det gør de ikke. De bliver bare hurtigere til at tælle. I stedet for flere regnestykker og hjælpemidler til at tælle længere, har eleverne brug for strategier. Eleverne skal introduceres for forskellige strategier og støttes i at udvikle et alsidigt repertoire af hukommelsesstrategier, så brugen af tællestrategierne med tiden fylder mindre og mindre i deres opgaveløsning. 

Undervisning med fokus på regnestrategier

En vigtig forudsætning for effektiv strategiundervisning er lærerens egen viden om regnestrategier. Udover at øge elevernes mængde af strategier, er det også vigtigt, at eleverne bliver bevidste om deres eget repertoire og valg af strategier. I undervisningen er det derfor vigtigt, at fokus i opgaverne flyttes fra resultatet til processen. Hellere meget kvalitet i arbejdet med få regnestykker end lidt kvalitet i arbejdet med mange. For at kunne støtte eleverne i deres strategiudvikling, er læreren nødt til at indhente viden om elevernes tænkning og strategibrug.

De første regnestrategier

Eleverne kan ikke flytte sig fra at tælle til at regne, før de kan nogle regnestykker udenad. Nogle af de første regnestykker, der kan være hensigtsmæssige at lære udenad, er plus-parrene (1+1, 2+2, 3+3 osv.) og 10’er vennerne (de to tal, som tilsammen giver 10). Eleverne kan lære at løse mange af de andre små regnestykker, når bare disse få regnestykker er automatiseret.

Plus-par
Plus-parrene kan bruges til de regnestykker, som er næsten det samme: “Når 6+6 giver 12, så må 6+7 give én mere, altså 13”. En anden regnestrategi, som anvender plus-parrene, kan være at omfordele regnestykker med forskellen to, så der dannes et plus-par: “Jeg kender ikke 7+5, men hvis jeg flytter én fra 7 over til 5, så bliver regnestykket 6+6, og det ved jeg giver 12”. 

10´er venner
På samme måde kan eleverne med 10’er vennerne løse de regnestykker, som er næsten det samme: “Jeg ved ikke, hvad 7+2 er, men når 7+3 bliver 10, så må 7+2 være én mindre, altså 9. 10’er vennerne kan også bruges til strategier, hvor eleverne fylder det ene tal op med 10’er vennen, og så bliver det 10+resten, for eksempel: “Jeg ved ikke, hvad 7+5 giver, men hvis jeg deler 5 op og lægger tre af dem over til de 7, så bliver det 10+resten, altså 10+2, og det giver 12. Det at kunne opdele tal, som her hvor 5 deles op i 3 og 2, er en vigtig forudsætning i arbejdet med regnestrategier, som derfor bør være en væsentlig del af arbejdet med kendskab og forståelse af tallene.

Der kan være flere forskellige strategier, som kan anvendes til samme regnestykke, men der er ikke én strategi, som passer til alle regnestykker. Derfor er det vigtigt med et bredt repertoire og en fleksibel tilgang, så eleverne kan vælge den smarteste vej i enhver situation.

Strategiudviklingen fortsætter, når tallene vokser

Efterhånden som eleverne lærer flere og flere regnestykker udenad, kan disse også benyttes i deres regnestrategier. Når tallene bliver større, kan eleverne fortsætte med at udvikle deres strategier til hovedregning ved at bevare den fleksible tilgang.

Ved et regnestykke som 27+25 tænker eleven måske på, at 25+25=50, så må 27+25 være to mere, altså 52. Ved regnestykket 48+26 kan eleven flytte to fra 26 over til 48, så bliver det i stedet 50+24, og resultatet er derfor 74. Eleven kunne også tænke, at 48+26 næsten er det samme som 50+26=76. Så har eleven lagt to for meget til, og resultatet må derfor være to mindre end 76, altså 74. 

Bevar fleksibiliteten i arbejdet med regnemetoder

Når der arbejdes med regnemetoder, er det vigtigt at bevare fleksibiliteten. I stedet for at præsentere eleverne for mange forskellige opstillingsmetoder, kan læreren lade elevernes talforståelse og forskellige strategier være styrende gennem en fleksibel metode med plads til forskellige fremgangsmåder.

En åben tallinje
Til addition og subtraktion kan en fleksibel metode være at bevæge sig frem og tilbage på en åben tallinje. Det er en tallinje uden forhåndstrykte tal og opdelinger, hvor eleverne selv markerer, hvilket tal de starter på. Herfra kan eleverne tage så store eller små hop, som de nu kan overskue, og i den rækkefølge det falder dem mest naturligt.

© Maria Grove Christensen

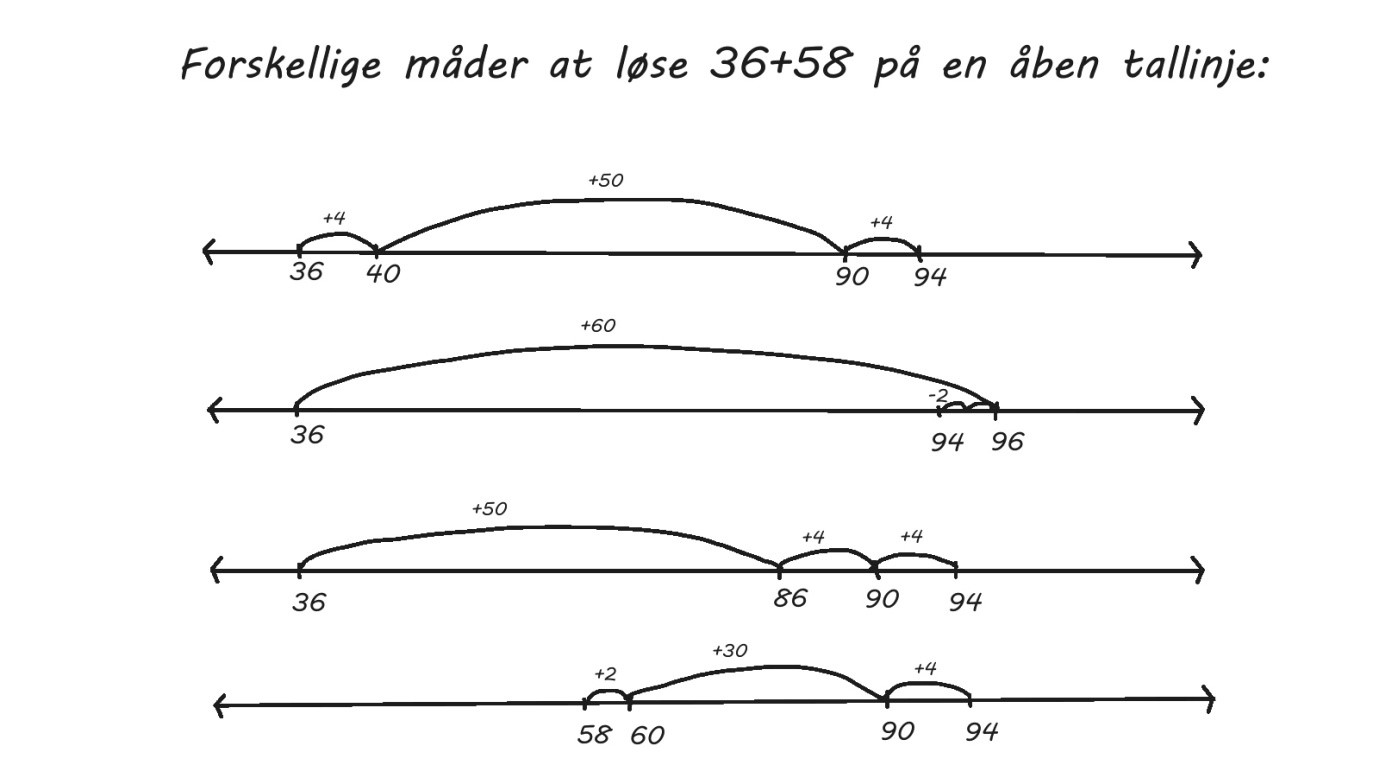
Lad eksempelvis alle i klassen skrive, hvilke hop de vil tage for at løse 36+58. Herefter kan I tale sammen for at se, hvor mange forskellige måder, eleverne har gjort det på. Eleverne kan forklare, hvordan de har tænkt, og de kan lytte til de andres forklaringer. Måske bliver de inspireret til nye tilgange. Det smarte ved fleksible metoder som denne er, at eleverne kan blive bedre og bedre inden for metoden, og samtidig er der plads til at benytte den strategi, som passer bedst til hvert stykke. Det er eleverne, der med afsæt i deres talforståelse og regnestrategier, træffer de valg, som udfylder metoden. På den måde udvikler eleverne både deres forståelse og regnefærdigheder på samme tid.

 

Det videre arbejde med regnestrategier

© Maria Grove Christensen

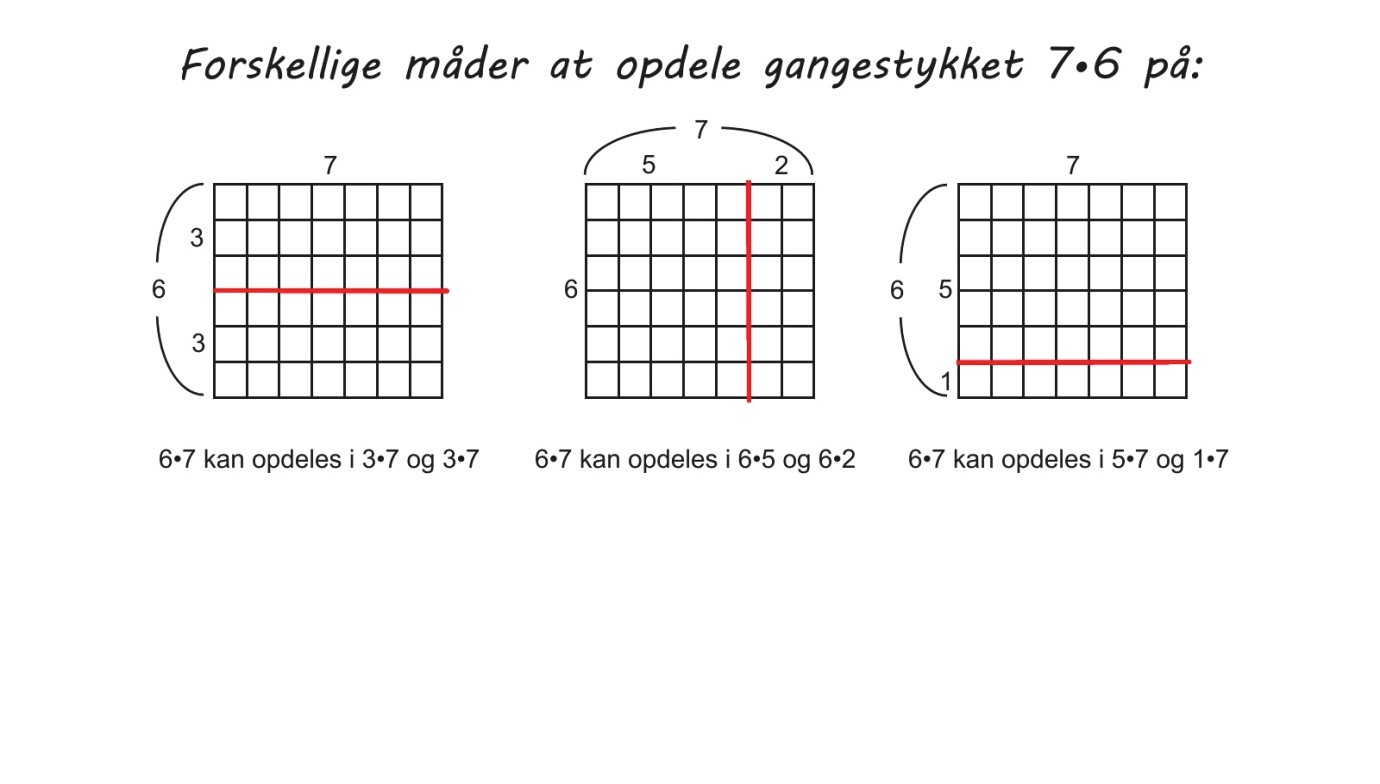
Når det kommer til arbejdet med multiplikation og division, skal tilgangen være den samme. Først skal eleverne have grundlagt en forståelse af regnearterne ved at tælle sig frem i bundter og dele ud én ad gangen. Det er godt at lære tabelremserne, men brugen af tabelremser er stadig en tællestrategi. Først når eleverne har lært nogle af regnestykkerne udenad, har de mulighed for at rykke sig til hensigtsmæssige hukommelsesstrategier, hvor de deler regnestykket op og trækker på deres faktaviden. Hvordan det er hensigtsmæssigt for den enkelte elev at opdele regnestykket afhænger af, hvilke regnestykker eleven kan udenad.

 

Forslag til fælles refleksion i skolens fagteam

Herunder er listet ideer til, hvordan fagteamet med udgangspunkt i konkrete spørgsmål kan sætte fokus på arbejdet med regnestrategier:

• Gennemgå i fællesskab regnestrategierne fra oversigten. På hvilken måde indgår arbejdet med disse strategier i jeres undervisning? Del ideer til undervisningsaktiviteter, som er gode til at flytte fokus fra resultatet til de anvendte regnestrategier.
• Hvordan kan teamet hjælpe hinanden med at ”parkere sine egne favoritter” og åbne op for fleksible regnemetoder og en bred vifte af regnestrategier i undervisningen?
• Hvordan kan matematikvejlederen bidrage til fælles fodslag og rød tråd i arbejdet med talforståelse, regnestrategier og regnemetoder gennem hele skoleforløbet? 

 

Inspiration

Artikel om tidlig algebra: Tidlig algebra

Artikel om talforståelse: Talforståelse

Læs også om talforståelse og regnestrategier i faghæftet for matematik, som du finder her: Faghæfte - Fælles Mål, læseplan og vejledning

Læs om udviklingen i indholdet i undervisningen inden for området Tal og algebra.

• 1.trinforløb, 1.-3. klassetrin, s. 37
• 2.trinforløb, 4.-6-.klassetrin, s. 44-45
• 3.trinforløb, 7.-9. klassetrin, s. 52
• De matematiske stofområder: Brudstykker af talarbejdet på de yngste klassetrin, s. 76-77

Opmærksomhedspunkter efter 3. klassetrin:

• Eleven kan addere og subtrahere enkle naturlige tal med hovedregning og lommeregner.
  (Tal og algebra/Regnestrategier).s. 62

Opmærksomhedspunkter efter 6. klassetrin:

• Eleven kan vælge hensigtsmæssig regningsart til løsning af enkle hverdagsproblemer og opstille et simpelt regneudtryk (Tal og algebra/Regnestrategier). S. 63
• Eleven kan gennemføre regneprocesser inden for alle fire regningsarter med inddragelse af overslag og lommeregner. (Tal og algebra/Regnestrategier). S. 63

Opmærksomhedspunkt på 7.-9. klassetrin

• Eleven kan gennemføre simple procentberegninger med overslag og lommeregner
  (Tal og algebra/Regnestrategier). S. 63

 

 

Kreditering

Artiklen er skrevet af Maria Grove Christensen, konsulent og lærermiddelforfatter samt lærer og matematikvejleder på Sofiendalskolen i Aalborg.