Talforståelse

Generelt bruges tal på fire forskellige måder:

1. Tal bruges til at beskrive størrelsen på en mængde, som kardinaltal. Det kan handle om antallet af børn i en klasse, eller et antal mælketænder et barn har tabt.
2. Tal bruges også til at beskrive et elements relative placering, som ordenstal. Det kan handle om det tredje barn i en række eller den første tabte tand.
3. Tal bruges desuden til at angive størrelser som længde, tid og vægt, som måltal eller kvantiteter. Det kan dreje sig om et barns højde eller om størrelsen (arealet) af et klasselokale. Her tælles ikke et antal elementer, men et antal enheder.
4. Endelig bruges tal på ikke-numeriske måder, eksempelvis i telefonnumre eller på busruter.

Et aspekt af talforståelse handler om at få erfaring i at bruge tallene på forskellige måder i forskellige kontekster. Det kan eleverne gøre allerede fra begyndelsen af skoleforløbet. Læreren bør dog være opmærksom på, at når tallene bruges som måltal, bør det i begyndelsen være i sammenhæng med uformelle enheder, som gør det muligt at tælle sig frem. En gummistøvle kan bruge som længdeenhed og en bog som arealenhed.

Til refleksion: Overvej, hvor de fire forskellige måder at bruge tal på kan komme i spil i en 1. klasses hverdagsliv.

Talforståelse og tællestrategier

I praksis har eleverne brug for at kunne kombinere de forskellige måder at bruge tal på. Hvis eleverne vil finde ud af, hvor mange centicubes, der er i en bunke, kan de tælle dem. Når eleverne tæller, bruger de tallene som ordenstal, fordi der er én centicube, de kalder 1, én de kalder 2 osv. Den sidste centicube i bunken kalder de for eksempel 12, men eleverne er ikke interesserede i, at det er den 12. centicube i rækken. De bruger tallet 12 kardinalt til at beskrive, hvor mange centicubes der er i alt. At finde antallet af centicubes i en bunke kræver med andre ord forståelse for, at de 12 kan knyttes til den samlede mængde og ikke kun til den sidste centicube. Denne form for talforståelse kaldes kardinal integration (Fuson, 2003).

At finde antallet af elementer i en mængde kræver, at eleverne kan:

• tælleremsen
• knytte hvert ord i remsen til netop ét element i en mængde (én-til-én korrespondance)
• kardinal integration

De fleste børn har erfaringer med at bruge tælleremsen, når de begynder i skole. De er vant til at bruge tælleremser i forbindelse med lege og spil, og de fleste er også vant til at koordinere talord og ting, når de tæller (én-til-én korrespondance). Forskning tyder imidlertid på, at det er vanskeligere for børn i skolestartsalderen at foretage kardinal integration (Munn, 1997). Elever, der kan et langt stykke af tælleremsen, og som kan forbinde talord og ting, kan altså ikke nødvendigvis løse en opgave, hvor de bliver bedt om at give et bestemt antal klodser til en klassekammerat.

Ifølge Munn skyldes dette, at børn sjældent tæller for at bestemme en mængdes størrelse, men mere som en del af lege eller en remse de øver sig på. Disse lege og øvelser er et godt grundlag for skolens undervisning i talforståelse. Det er dog vigtigt, at eleverne også bliver inddraget i aktiviteter, hvor det giver mening for dem at finde frem til et antal, så de både skal bruge tælleremsen, én-til-én korrespondance og kardinal integration. Sådanne situationer kan være tæt forbundet med spil, lege med bevægelse og klassens hverdagsliv. Det kan handle om at finde ud af:

• hvor mange børn, der er på hvert hold.
• hvor mange kegler, der er væltet.
• hvor mange børn, der er 6 år, 7 år eller 8 år.
• hvor der er flest…
• hvor mange, der er i alt…

Til refleksion: Overvej, hvordan elever i 1. klasse kan bestemme antal i meningsfulde situationer.

Talforståelse og konkrete materialer

I begyndelsen af skoleforløbet bør eleverne have rige muligheder for at bruge tal i konkrete sammenhænge. Det er imidlertid også hensigten, at eleverne gradvist kommer til at opfatte tallene som objekter i sig selv. Det betyder, at hvert tal ikke alene har mening i sammenhæng med ting, der skal tælles, men også giver mening i kraft af sine relationer til andre tal. Eksempelvis kan eleverne komme til at opfatte tallet 12 som:

• et lige tal
• det dobbelte af 6
• et tal, der består af 1 tier og 2 enere
• et tal, der svarer til 10 + 2

Eleverne kan udvikle en sådan forståelse af de naturlige tal, når de bliver involveret i undersøgelser, der giver dem mulighed for at opdage egenskaber ved tallene. Det er afgørende, at sådanne undersøgelser understøttes af konkrete materialer og elevernes egne tegninger.

Det kan dreje sig om, at:

© Børne- og Undervisningsministeriet

Forståelse af titalssystemet

Elevernes forståelse af titalssystemet er afgørende for deres muligheder for at udvikle metoder til beregninger. Titalssystemets grundlæggende ide er at gruppere enere i grupper af 10, tiere af grupper af 100 osv. Tallene angives ved at skrive hvor mange af hver type gruppe, det indeholder. Med andre ord: Hvor mange af hver tierpotens tallet indeholder.

I nogle lande hænger talordene sammen med titalssystemets grundlæggende ide. Hvis tallet 352 skulle oversættes direkte fra kinesisk til dansk, ville det hedde tre-hundrede-fem-ti-to (Jess m.fl., 2008). De sproglige forhold i Danmark kræver særlig opmærksomhed på, at eleverne tolker symbolet 352 som 3 hundreder, 5 tiere og 2 enere.

© Børne- og Undervisningsministeriet

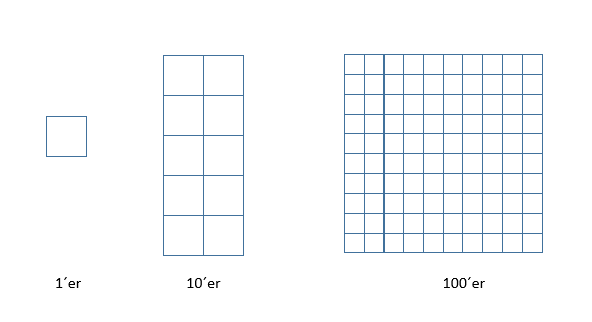
Eleverne kan få mulighed for at udvikle sådanne forståelser af titalssystemet samtidig med, at de udvikler metoder til addition og subtraktion, når deres arbejde understøttes med konkrete materialer eller tegninger. De konkrete materialer skal repræsentere 1´ere, 10´ere og (senere) 100´ere. Sådanne materialer kan købes eller fremstilles i klassen af eleverne selv. De kan bestå af papkort med kvadrater - se billede.

De konkrete repræsentationer af flercifrede tal kan give eleverne mulighed for at bygge videre på deres tællestrategier og deres viden om, at tal kan opdeles, når de udvikler metoder til addition med flercifrede tal.

I det følgende omtales tre forskellige tilgange til addition, som elever i 1.-2. klasse kan støttes til at udvikle (Fuson, 2003). Disse tilgange giver samtidig eleverne mulighed for at videreudvikle deres talforståelser:

• Tællemetoder (eksempel 46 + 38)
  
  Lucca bygger tallene med centicubes. Det ene tal har 4 tierstænger og 6 løse. Det andet tal har 3 tierstænger og 7 løse. ”Jeg ved, der er 46 her”, siger hun og peger. Nu tæller jeg videre: ”56, 66, 76”. Hun flytter en tierstang for hvert talord, hun siger: ”Nu har jeg talt alle tierne. Nu mangler jeg at tælle de sidste enere. 77, 78, 79, 80, 81, 82, 83, 84”. Hun flytter en centicube ad gangen.
  
  
• Opdelingsmetoder (eksempel 46 + 38)
  
  Albert bygger tallene med centicubes. Han samler de 4 og de 3 tierstænger i én bunke og enerne i en anden bunke: ”Jeg har 7 tiere og 14 enere”’, siger han. ”14 enere er 1 tier og 4 enere. Så bliver det 8 tiere og 4 enere i alt. Det er 84.”
  
  
• Omgrupperingsmetoder (eksempel 46 + 38)
  
  Frederikke siger: ”Hvis det havde været 46 plus 40, så ville det blive 86. Men nu er det 2 mindre end 86, for 38 er 2 mindre end 40.”

Til refleksion: På hvilke måder kan vi sige, at eleverne med de tre tilgange bygger videre på tællestrategier og viden om, at naturlige tal kan opdeles?

Fuson (2003) peger på, at tilgang 1 fungerer fint til tocifrede tal, men bliver lidt besværlig hvis tallene har flere cifre. Hun peger også på, at tilgang 3 fungerer bedst, når et af tallene er tæt på et helt antal tiere. Til gengæld siger hun, at tilgang 2 let kan generaliseres til større tal. Er vi enige? Hvilken vægt kan vi lægge på hver af de tre tilgange i undervisningen?

Hvordan kan eleverne støttes til at bygge videre på tilgang 2, så det bliver en metode til at addere med støtte i noter?

Inspiration

Artikel om tidlig algebra: Tidlig algebra.

Artikel om regnestrategier: Sæt fokus på regnestrategier og lær eleverne at tænke fleksibelt

Læs også om talforståelse og regnestrategier i i faghæftet for matematik, som du finder her: Faghæfte - Fælles Mål, læseplan og vejledning



Læs om udviklingen i indholdet i undervisningen inden for området Tal og algebra her:

• 1.trinforløb, 1.-3. klassetrin, s. 36-37
• 2.trinforløb, 4.-6-.klassetrin, s. 44-45
• 3.trinforløb, 7.-9. klassetrin, s. 51-52

Opmærksomhedspunkter efter 3. klassetrin:

• Eleven kan anvende trecifrede tal til at beskrive antal og rækkefølge.
  
  Tal og algebra/Tal). s. 62

Kreditering

Artiklen er udarbejdet af Thomas Kaas, lektor og ph.d. stipendiat.