Artikel
Bevægelse i matematikundervisningen
Flere undersøgelser har haft matematik som omdrejningspunkt i forhold til bevægelse med fokus på, at bevægelse i sig selv har skabt et øget fagligt udbytte. Her gives et bud på et matematisk fokus i bevægelsen.
Skolereformen i 2013 indebar et krav om, at eleverne får motion og bevægelse i gennemsnit 45 minutter om dagen i undervisningstiden. Megen forskning begrunder, at elever, der er fysisk aktive i en periode, lærer mere og bedre end en tilsvarende fysisk passiv elevgruppe. Derudover har forskningen også vist, at inddragelse af bevægelsesaktiviteter skaber en variation i undervisningen, hvilket kan øge motivationen for deltagelse hos eleverne betragteligt.
I de følgende afsnit er bevægelsesaktiviteter i matematikundervisningen forstået som aktiviteter med et tydeligt matematikfagligt indhold, der kan relateres til elementer i Fælles Mål, og hvor eleverne er kropsligt aktive i større eller mindre grad. De bagvedliggende begrundelser for tilgangen i denne artikel er et fokus på, at eleverne kan lære med hele kroppen, og at læring sker gennem refleksion over de aktiviteter, eleven inddrages i.
Matematiklæring i fokus
Bevægelsesaktiviteter kan være med til at øge elevernes matematiklæring, hvis læreren holder fokus på det matematiske indhold i aktiviteterne. Det betyder at:
- formålet med enhver bevægelsesaktivitet i matematikundervisningen skal kunne relateres til matematikfaget.
- eleverne skal både før, under og efter bevægelsesaktiviteten støttes i at holde fokus på det matematiske indhold for at sikre, at der sker matematiklæring.
Det betyder ikke, at der ikke med stor relevans kan laves andre former for bevægelsesaktiviteter. Blot vil det ikke her blive set som matematikundervisning.
Før en bevægelsesaktivitet
Tydelighed over for eleverne kan sikres ved at starte med at italesætte aktiviteten og dens matematiske fokus. Det kan foregå gennem en tydelig rammesætning af aktiviteten og dens matematiske indhold og formål, eksempelvis at eleverne skal:
- opnå erfaringer med et nyt matematisk begreb.
- opnå erkendelser om matematiske sammenhænge.
- undersøge en matematisk problemstilling.
- generere data til videre bearbejdning.
Under en bevægelsesaktivitet
Under aktiviteten kan læreren gennem en undersøgende dialog understøtte elevernes fokus på det matematiske indhold. Fokus er forskelligt, alt efter hvilke(n) af ovennævnte fire formål, eleverne skal arbejde indenfor. Herunder uddybes de fire ovenstående formål med konkrete eksempler:
1. At opnå erfaringer med et nyt matematisk begreb
Et ønske om at skabe forståelse for forskellige aspekter af multiplikation, eksempelvis 4 x 6, kan tage afsæt i at lave 4 rækker af 6 skoletasker, hvilket kan ses som den klassiske gentagende addition. Klassen kan også se på skoletaskerne som 6 grupper af 4 tasker og omvendt, hvilket svarer til en arealforståelse for multiplikation. Gennem samtale og spørgsmål kan eleverne rette fokus mod de centrale matematiske elementer af begrebet - her forskellige forståelser af multiplikation.
Efterfølgende kan aktiviteten udvides ved at få eleverne til at omgruppere taskerne til andre multiplikationsstykker. Der kan også spørges til, hvor mange måder 4 elever hver kan tage en af 6 skoletasker, hvorved det kombinatoriske aspekt af multiplikationen kommer ind i billedet (som dog ikke besvares med 6 X4
2. At opnå erkendelser om matematiske sammenhænge
Eleverne kan i denne aktivitet opnå en erkendelse af sammenhængen mellem positionerne i titalssystemet. Eleverne skal i grupper på tre hente tællematerialer, svarende til et trecifret tal på en keglebane. Når hele klassen er i gang, bruges flere keglebaner. Banen består af tre linjer, der hver er markeret med en start- og en slutkegle. Ved hver slutkegle står en kasse med tællemateriale, der repræsenterer henholdsvis enere, tiere og hundrede:
- Den 1. linje er 30 centimeter lang. Her skal enerne i tallet tælles, så tællematerialet ved slutkeglen repræsenterer enere og så fremdeles.
- 2. linje har en afstand på 3 meter mellem de to kegler. Her skal tiercifferet tælles.
- 3. linje har 30 meter mellem de to kegler, og her skal hundredcifferet tælles.
Grupperne får udleveret hver et trecifret tal. Hver elev i gruppen skal så hente tællemateriale, et ad gangen, langs den linje, der svarer til elevens positions ciffer.
Eksempel: Med tallet 253, skal eleven ved 3-centimeterlinjen, hvor der hentes enerne, dermed gå tre gange. Eleven ved 3-meterlinjen, hvor der hentes tiere, skal gå fem gange osv. Eleven på 30-centimeter-linjen bliver naturligvis hurtigst færdig. Eleven kan så hjælpe eleven på 3-meterlinjen ved at hente 20 ekstra enere på sin egen linje. Disse enere kan veksles til, at eleven på 3-meterlinjen skal hente 2 færre tiere. Ligeledes kan eleven på tierlinjen hente 10 ekstra tiere på sin linje og dermed hjælpe eleven på 30-meterlinjen, så denne elev kun skal gå 1 gang. Eleverne skal altså samarbejde om hurtigst muligt at hente tællemateriale svarende til det samlede tal ved at veksle mellem enere, tiere og hundrede.
Dialogen med eleverne skal i sådanne aktiviteter ledes hen imod relationerne mellem positionerne. Der kan tales om, hvad de hver især udtrykker, og at når der er fyldt op til 10 i en position, giver det 1 ekstra i næste position. Der er vigtigt, at dialogen også peger ind i efterbehandlingen, så eleverne senere vil kunne danne koblinger mellem denne aktivitet og andre tilsvarende aktiviteter eller opgaver.
Et andet eksempel på arbejdet med erkendelse af sammenhænge kan være at lade eleverne gå langs en side på kvadrater med forskellige sidelængder, hvor de tæller antal ”normale” skridt. Efterfølgende kan eleverne gå langs diagonalen for at finde ud af, at diagonalen i et kvadrat altid er ca. 1,4 gange så lang som sidelængden. Mere præcist er forholdet 2, hvilket kan være pointen i et dybere matematisk arbejde i Geogebra eller ved hjælp af Pythagoras sætning, som efterbehandling på aktiviteten.
3. At undersøge en matematisk problemstilling
Eleverne kan undersøge antallet af diagonaler i en polygon ved at sparke en bold til hinanden, så enten afsender eller modtager er forskellig hver gang - og uden at sparke bolden til dem lige ved siden af. De kan også undersøge, hvor mange måder de kan gå op ad en trappe på ved enten at tage et eller to trin ad gangen eller ved en kombination af disse.
Fælles for begge øvelser er, at eleverne skal støttes i at gå fra lidt tilfældigt at afprøve forskellige måder at gå eller sparke på, til at gennemføre en mere systematisk undersøgelse. Den systematiske undersøgelse kan igangsættes ved at rette elevernes fokus mod en simplere version af problemet, eksempelvis ved at undersøge en femkant frem for en syvkant, eller en femtrinstrappe frem for en tolvtrinstrappe.
Der kan spørges ind til, hvilke sammenhænge eleverne ser mellem deres resultater. Der kan arbejdes hen i mod, at eleverne udvikler et skema ordnet efter antal kanter i polygonen eller efter antal trin på trappen, for at støtte deres refleksioner. Et eksempel som dette kan der også henvises til i efterfølgende undersøgelsesaktiviteter som en fælles erfaring med at strukturere undersøgelser
4. At generere data til videre bearbejdning
Det kan eksempelvis undersøges, hvor langt eleverne kan støde i kuglestød med tre forsøg hver. Der vil så blive genereret en række data, som eleverne efterfølgende kan lave statistik på med fokus på udvalgte deskriptorer. Der kan også laves markeringer ved nedslaget af de enkelte stød. Ud fra disse markeringer kan eleverne diskutere medianen, kvartilsættet og største-/mindsteværdi, og dermed kan de visualisere et boksplot med de faktiske data på stedet. Det centrale i disse aktiviteter er at have fokus på selve datagenereringen, så der indsamles gode data til den videre bearbejdning.
Læreren kan naturligvis vælge mange andre aktiviteter, eleverne skal gennemføre og måle på: løb, gang, kravl, cykling, spring og antal kast til hinanden. En variant af ovenstående er at lave stopdans. Høj danseintensitet i et kort interval, og når musikken stopper, fryser eleverne. Her kan der stilles spørgsmål til klassen som: Hvilken brøkdel/andel af klassen står på et ben? - har hovedet på skrå? Eller peger mod loftet?
Efter en bevægelsesaktivitet
Efterbehandlingen af undervisningsaktiviteter er helt central. Det er her, udbyttet af aktiviteten gennem refleksion skal gøres til erfaring og dermed fastholdes som læring hos eleverne. Herunder beskrives et eksempel på efterbehandling ud fra en konkret aktivitet, hvor eleverne skulle løbe en graf.
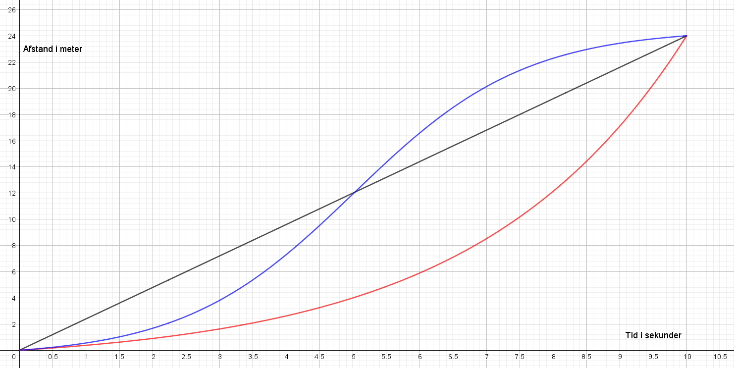
Opgave: Eleverne får udleveret en graf med tre kurver på. Det er tid/sted-kurver, der svarer til hver sin måde at bevæge sig 24 meter på i forhold til fart. Eleverne skal nu reproducere de tre løb og filme dem, således de passer med grafen.
Det er i efterbehandlingen af denne aktivitet, at eleverne gennem dialog kan skabe matematiske erfaringer med noget, der svarer til de tre matematiske vækstformer: logistisk vækst (blå) og særligt den lineære(sort) - og den procentuelle (rød) vækst. Dette kan ske gennem refleksion over, hvordan eleverne skulle bevæge sig, for at det svarede til grafen. Pointerne er, at den lineære vækst svarer til at bevæge sig med konstant fart, hvorimod eleverne hele tiden skulle løbe hurtigere og hurtigere for at følge kurven svarende til den procentvise vækst. Efterbehandlingen kunne også lade eleverne fortsætte kurverne og give bud på, hvor hurtigt de skulle løbe, hvis de fortsatte yderligere 10 sekunder efter samme vækstformer.
Fælles arbejde blandt matematiklærere
Arbejdet med at bringe bevægelse ind i matematikundervisningen er ikke kun op til den enkelte matematiklærer. Det kan med fordel tages op som en drøftelse i fagteamet. Nedenfor er listet en række spørgsmål, teamet kan tage udgangspunkt i, hvis lærerne vil undersøge mulighederne for at lave gode bevægelsesaktiviteter på egen skole:
- Hvilke muligheder for matematiske undersøgelser med bevægelse giver området omkring vores skole?
- Hvilke matematiske begreber og sammenhænge har vi særlige rammer for at udvikle på igennem bevægelsesaktiviteter?
- Hvilke data kan vi skabe mulighed for, at eleverne indsamler gennem bevægelsesaktiviteter?
- Hvordan støtter vi eleverne i at fastholde et matematisk perspektiv, særligt under - og i efterbehandlingen af bevægelsesaktiviteten?
Eksempler vidensdeling og drøftelse af aktiviteter, som teamet har afprøvet:
- Hvilke matematiske indsigter har eleverne mulighed for at opnå igennem udførelse af disse aktiviteter, særligt set i forhold til Fælles Mål?
- Giver aktiviteten blot mulighed for træning af en given færdighed? Rummer aktiviteten mulighed for erkendelse af nye matematiske begreber? På hvilken måde er eleverne i gang? Er de i gang i korte eller lange intervaller? Er der perioder med megen stilstand - med eller uden matematisk refleksion?
- Motiverer aktiviteterne eleverne til arbejde med matematik?
- Kan udvikle opgaver fra lærebøger til bevægelsesaktiviteter?
På baggrund af drøftelser som ovenstående har fagteamet bedre mulighed for at skabe kvalificeret matematikundervisning, hvor bevægelse inddrages med øget variation og motivation i undervisningen til følge.
Inspiration
Artikel om forskningsprojekt med udgangspunkt i bevægelse i matematikundervisningen: Brug kroppen - lær mere
Konkrete ideer til brug af brain breaks i undervisningen: Brain breaks kan styrke elevernes læring
Læs også om arbejdet med bevægelse i faghæftet for matematik, som du finder her: Læseplan og vejledning
Kreditering
Artiklen er udarbejdet af Henning Westphael, Lektor, underviser i matematik, VIA -Læreruddannelsen i Århus. Cand. Scient.
Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.