Tidlig algebra - Matematik - GRUNDSKOLE

Tidligere var algebra et fagområde, som begyndte senere i skoleforløbet. Forskning tyder imidlertid på, at eleverne udvikler bedre forståelse og kunnen inden for algebra, hvis de får mulighed for at ’tænke algebraisk’ i sammenhæng med fagets andre fagområder allerede fra begyndelsen af deres skoleforløb (Brizuela, Martinez, & Cayton-Hodges, 2013). Denne nye tilgang til algebraundervisning kaldes ’tidlig algebra’ (Carraher & Schliemann, 2007).

Traditionelt har algebra først og fremmest været forbundet med at ’manipulere med bogstaver’ for at løse ligninger eller for at reducere bogstavudtryk. I tidlig algebra er forståelsen af, hvad der kendetegner algebra, bredere og dybere. Indholdet i tidlig algebra kan beskrives med to kerneelementer, der betegner bestemte former for ’algebraisk tænkning’ (Kaas, 2019):

at generalisere egenskaber og sammenhænge
at ræsonnere med ukendte talstørrelser

At generalisere matematiske egenskaber

Når man adderer to ulige tal, får man et lige tal. Mange elever opdager denne egenskab ved naturlige tal, hvis de arbejder med at addere ulige tal, og læreren kan rette deres opmærksomhed mod resultaterne med spørgsmål som:

Er der et mønster?
Har resultaterne noget tilfælles?
Bliver resultaterne også ulige tal?

Næste fokuspunkt kan være, om det mon altid gælder, at summen af to ulige tal er et lige tal? Hvorfor eller hvorfor ikke?

Ændringen fra at fokusere på de konkrete eksempler til at fokusere på, om egenskaben gælder for en hel mængde af tal, for eksempel alle de naturlige tal, er en bevægelse mod at generalisere. En matematisk generalisering involverer en påstand om, at en egenskab holder for en stor mængde af matematiske objekter (Carraher m.fl., 2008).

Eksempel: 1. klasse

Elever kan allerede fra 1. klasse opdage, repræsentere og begrunde sådanne generaliseringer i forbindelse med beregninger. De kan opdage, at rækkefølgen af addenderne ikke har betydning, når de adderer. Udgangspunktet kan være almindelige plusstykker, der står i en rækkefølge, så eleverne får mulighed for at se ensartetheden:

9 + 5

5 + 9

8 + 7

7 + 8

Eleverne kan udtrykke (repræsentere) sådanne opdagelser på forskellige måder. I 1. klasse vil det være oplagt, at eleverne fortæller med egne ord, hvad de lægger mærke til og om de hypoteser, det giver anledning til. Eksempler kan være: ’Resultaterne bliver det samme, selv om tallene er byttet om’, eller ’du kan plusse tallene i den rækkefølge, du vil’.

Igennem klassesamtale kan eleverne komme til at tænke dybere om en sådan hypotese igennem spørgsmål som:

Gælder det mon altid?
For hvilke tal gælder det? Gælder det for store tal? For små tal?

Desuden kan eleverne guides i retning af at repræsentere deres opdagelse på nye måder og mod at begrunde den gennem spørgsmål som:

Kan I vise jeres opdagelse med centicubes?
Hvordan kan I vide, at den er rigtig?
Hvordan vil I forklare nogen, at den passer?

I eksemplet repræsenterer og begrunder eleverne deres opdagelse af den kommutative egenskab for addition på uformelle måder. De bruger deres naturlige sprog, og deres begrundelser bygger på overbevisende eksempler. Igennem skoleforløbet sigter undervisningen i algebra blandt andet på, at eleverne kommer til at repræsentere generaliseringer med bogstavsymboler.

At bruge bogstavudtryk til at repræsentere generaliseringer i 1. klasse

Opdagelsen af, at rækkefølgen af addenderne ikke har betydning ved addition, kan repræsenteres som a + b = b + a, hvor ^a og ^b er reelle tal. Forskning viser, at det er muligt for elever allerede i indskolingen at udvikle forståelse for variable og for at anvende bogstavudtryk til at repræsentere generaliseringer (Blanton, Brizuela, Gardiner, Sawrey, & Newman-Owens, 2017). Ideen om at udtrykke generelle sammenhænge og egenskaber med bogstavudtryk kan derfor godt introduceres tidligt. Det kan være en mulighed side om side med muligheden for at udtrykke sig med mere uformelt sprog. For nogle elever kan det endda vise sig, at de ret hurtigt har lettere ved at udtrykke generaliseringer med algebraiske symboler end med uformelt sprog.

Eksemplet handler om generalisering i forbindelse med beregninger. Der er mange andre opdagelser af samme type, som eleverne kan gøre sig igennem deres første skoleår, eksempelvis:

Når du ganger to tal, har rækkefølgen ikke betydning (a · b = b · a).
Når du adderer tre tal, kan du addere de to første to og derefter det sidste, eller du kan addere de sidste to og derefter det første (a + b) + c = c + (b + c).
Når du ganger et tal med 1, får du det samme tal (a · 1 = a).
Når du adderer to lige tal, får du et tal, der også er lige (2m + 2n = 2(m + n)).

At generalisere matematiske sammenhænge

En anden type generaliseringer handler om sammenhænge mellem tal, der varierer. I 2. klasse kan det dreje sig om sammenhængen mellem den ene sidelængde og det antal kvadrater, der er ’inden i’ i rektangel, som har en fast sidelængde på 2.

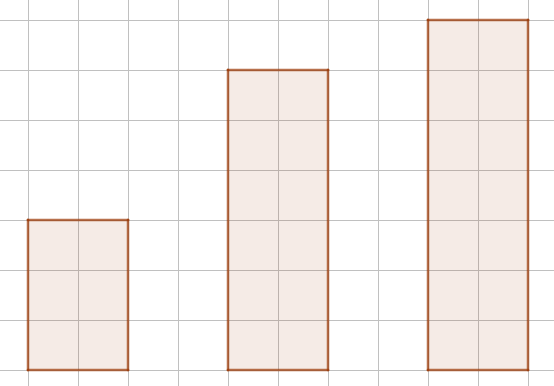
Når den ene sidelængde varierer, ændrer antallet af kvadrater sig. Der er med andre ord en funktionel sammenhæng mellem denne sidelængde og arealet. Denne sammenhæng gælder for alle rektangler, der har en fast sidelængde på 2.

Eksempel: 2. klasse

Undervisningen kan begynde med, at eleverne på kvadratpapir tegner rektangler, der har en fast sidelængde på 2. De kan frit vælge den anden sidelængde. Der kan tages udgangspunkt i spørgsmål som:

Hvor mange firkanter kommer der inden i hvert rektangel? Hvordan finder I ud af det?
Kan I finde ud af det uden at tælle alle firkanterne? Er der en måde, I kan bruge hver gang?

Nogle elever kan opdage, at de i et rektangel med sidelængden 5 kan finde antallet af firkanter inden i ved at regne 5 + 5. Hvis sidelængden er 6, er det 6 + 6. Elevernes resultater kan samles i en tabel på klassens tavle:

Sidelængde	Antal firkanter
1	2
2	4
3	6
4	8
5	10

Tabellen kan danne udgangspunkt for elevernes opdagelser af mønstre. Tallene i den højre kolonne udgør her en talfølge, som vokser med 2 fra trin til trin. Det ’vandrette mønster’ er den generelle sammenhæng mellem sidelængde og areal i rektanglerne. Igen kan eleverne formulere sammenhængen i deres naturlige sprog: Der er dobbelt så mange firkanter.

At bruge bogstavudtryk til at repræsentere generaliseringer i 2. klasse

På sigt kan eleverne formulere sammenhængen i ovenstående eksempel med brug af bogstaver, som f = s + s.

Læreren kan udfordre påstanden for at give eleverne mulighed for at udvikle deres algebraiske tænkning gennem spørgsmål som:

Passer det i hele tabellen, at antallet af firkanter er dobbelt så stort som sidelængden? Vil det passe altid? Hvorfor?
Hvordan passer det med den måde, I regnede på, da I tegnede rektanglerne?

Der er mange andre sammenhænge, som eleverne kan opdage, repræsentere og begrunde på tilsvarende måder. Det kan være sammenhængen mellem:

antal børn og antal øjne.
antal centicubes og antal sideflader i ’centicubestænger’.
antal borde og antal stole i forskellige bordopstillinger.

De nævnte eksempler udgør alle sammen funktioner. Senere kan sådanne sammenhænge repræsenteres med grafer i et koordinatsystem og repræsenteres med funktionsforskrifter. Arbejdet med tidlig algebra giver derfor mulighed for at skabe en rød tråd igennem hele skoleforløbet i arbejdet med funktioner.

At ræsonnere med ukendte talstørrelser

Det andet kerneelement i algebraisk tænkning handler om at ræsonnere i situationer, hvori der indgår et eller flere ukendte tal.

Eksempel: 3. klasse

I 3. klasse kan en sådan situation være:

Iskiosken ’Vaflen’ sælger isvafler, hvor hver kugle koster 5 kroner. Du skal også betale for vaflen. Den koster 9 kroner. Iskiosken ’Ismejeriet’ sælger isvafler, hvor hver kugle koster 8 kroner. Du skal ikke betale for vaflen. Hvor kan det bedst betale sig at købe isvafler?

Her skal eleverne ikke opdage en generel sammenhæng. Relationen mellem antal kugler og pris i hver iskiosk er givet på forhånd. Det er snarere elevernes opgave at oversætte beskrivelsen af disse relationer til ’matematiksprog’, som gør det muligt at ’regne på sagen’. En sådan oversættelse kan opstilles i en tabel:

*Vaffel og antal kugler*	*Iskiosken Vaflen (kr.)*	*Iskiosken Ismejeriet (kr.)*
1	14	8
2	19	16
3	24	24
4	29	32

Andre oversættelser kan være til en punktgraf i et koordinatsystem eller til tegninger af isvafler med forskellige antal kugler suppleret med tal, der viser priser.

At bruge bogstavudtryk til at repræsentere generaliseringer i 3. klasse og senere

Det er hensigten, at eleverne på senere klassetrin oversætter situationen til algebraisk symbolsprog. I en sådan oversættelse kan antallet af iskugler repræsenteres med n, og der kan opstilles en ligning, hvis løsning bidrager til at svare på opgaven:

5n + 9 = 8n

Oversættelsen omfatter nogle beregninger. Hvis nogle elever vil løse opgaven ved at opstille en ligning, må de løse ligningen. Hvis nogle elever vil løse opgaven ved at opstille en tabel, må de foretage beregninger, når de udfylder tabellen. Endelig må resultatet tolkes i forhold til situationen. Ligningens løsning (3) betyder, at det koster lige mange penge i hver kiosk at købe en isvaffel med 3 kugler. Tabellen viser, at det bedst kan betale sig at købe isvafler med 1 eller 2 kugler i iskiosk A og isvafler med mere end 3 kugler i iskiosk B.

Sammenfatning

Eksemplerne i denne artikel viser, hvordan tidlig algebraisk tænkning kan foregå i tæt sammenhæng med elevernes øvrige arbejde med matematik. Eleverne kan arbejde med generaliseringer, når de udvikler metoder til beregninger, og de kan arbejde med ræsonnementer med ukendte tal, når de arbejder med problemer, som vedrører en kontekst fra omverdenen. På den måde behøver tidlig algebra ikke at være et fagområde, som ’kommer oveni’ de øvrige fagområder. Det kan derimod ’flette sammen’ med de øvrige fagområder. Forskning viser, at der især er gode erfaringer med at ’flette’ de to kerneelementer i tidlig algebraisk tænkning sammen med stofområderne ’Tal og algebra’ og ’Funktioner’.

Modellen sammenfatter således nogle karakteristiske, forskningsbegrundede tilgange til tidlig algebra.

Modellen kan bruges som et pejlemærke i forbindelse med planlægning af undervisning i tidlig algebra. Det gælder om at skabe mulighed for, at eleverne opdager, repræsenterer og begrunder generelle matematiske sammenhænge og egenskaber. Det gælder også om at skabe muligheder for, at eleverne oversætter, beregner og tolker i situationer, hvor der indgår ukendte størrelser.

Centrale spørgsmål til diskussion i teamet kan være:

Kender vi aktiviteter/opgaver, som giver sådanne muligheder?
Kan vi ændre/tilpasse nogle opgaver, som giver sådanne muligheder?
Hvilke spørgsmål kan vi stille i klassen for at skabe sådanne muligheder?
Hvordan kan vi forestille os at bruge elevernes ideer og opdagelser i undervisningen?

Inspiration

Artikel om talforståelse: Talforståelse (emu.dk)

Artikel om regnestrategier: Sæt fokus på regnestrategier og lær eleverne at tænke fleksibelt (emu.dk)

Læs også om talforståelse og regnestrategier i i faghæftet for matematik, som du finder her: Faghæfte - Fælles Mål, læseplan og vejledning

Læs om udviklingen i indholdet i undervisningen inden for området Tal og algebra her:

1.trinforløb, 1.-3. klassetrin, s. 38
2.trinforløb, 4.-6-.klassetrin, s. 45
3.trinforløb, 7.-9. klassetrin, s. 52-53

Opmærksomhedspunkter efter 3. klassetrin:

Eleven kan anvende trecifrede tal til at beskrive antal og rækkefølge

(Tal og algebra/Tal). s. 62

Læs også temaet om Algebra på de yngste klassetrin på matematikdidaktik.dk

Siden matematikdidaktik.dk er udarbejdet af NCUM - Nationalt Center for Udvikling af Matematikundervisning.

Kreditering

Artiklen er udarbejdet af Thomas Kaas, lektor og ph.d. stipendiat.