Problemløsningskompetence og modelleringskompetence i matematikundervisningen

Der er efterhånden gennemført mange udviklingsprojekter, som underbygge følgende konklusioner:

• Refleksioner blandt og kommunikation mellem lærere og kursister om kernen i forskellige matematiske kompetencer kan potentielt fremme mange ønskværdige typer arbejdsprocesser i matematikundervisningen.
• I den forbindelse er det frugtbart at arbejde med matematisk modelleringskompetence og matematisk problemløsningskompetence som to kompetencer hvis læringsmæssige kerne er væsensforskellig.
• En del af potentialet ved at gøre sig de to kerners forskellighed klart består i, at det kan fokusere måden lærere inviterer deres kursister til at udvikle hver af de to kompetencer, fx gennem formulering og/eller udvælgelse af skriftlige opgaver.

I denne artikel, som er en forkortet og avu-tilpasset udgave af Jensen (2009), konkretiserer og eksemplificerer jeg disse konklusioner.

Det sker som det første ved at fremlægge min forståelse af kernen i hver af de to kompetencer. Derefter kommer jeg med konkrete eksempler på opgaver, som dels tydeliggør kompetencernes forskellighed, dels efter min vurdering vil være velegnede til at igangsætte kursisternes udvikling af dem i forbindelse med avu-matematikundervisning.

Matematisk modelleringskompetence

Kort og unuanceret handler denne kompetence om at kunne håndtere matematikbeskrivelser af noget der i udgangspunktet ikke er matematisk.

Mere præcist bruger jeg matematisk modelleringskompetence som betegnelse for nogens indsigtsfulde parathed til selv at gennemføre alle dele af en matematisk modelleringsproces og til at forholde sig kritisk undersøgende til andres ageren i den henseende (Jensen, 2007, s. 126).

Denne karakteristik bliver først for alvor interessant, hvis den suppleres med en beskrivelse af, hvad man forstår ved ”en matematisk modelleringsproces.”

Den matematiske modelleringsproces

© Børne- og Undervisningsministeriet

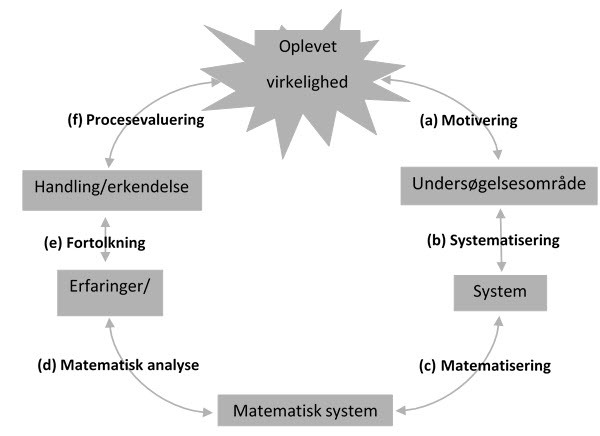
Figur 1. En visuel repræsentation af en model af den matematiske modelleringsproces (Jensen, 2009).

Modellen, og alle de begreber der indgår, er grundigt diskuteret og kommenteret i Jensen (2007, s. 107ff). I artiklen her supplerer jeg med et eksempel, men først efter også at have bragt matematisk problemløsningskompetence i spil, så jeg kan bruge eksemplet som led i at diskutere de to kompetencers forskellige kerne.

Matematisk problemløsningskompetence

Kort og unuanceret handler denne kompetence om at kunne håndtere en situation, hvor man for at komme videre skal finde på et eller andet der ikke lige springer i øjnene (Jensen, 2007, s. 120).

Mere præcist bruger jeg matematisk problemløsningskompetence som betegnelse for nogens indsigtsfulde parathed til selv at løse såvel rene som anvendelsesorienterede matematiske problemer og til at forholde sig kritisk undersøgende til andres ageren i den henseende (Jensen, 2007, s. 126).

I KOM-rapporten (Niss & Jensen, 2002, s. 49-50) kombineres denne kompetence med det at kunne opstille matematiske problemer, hvilket betegnes matematisk problembehandlingskompetence.

Det centrale begreb at få hold på i forbindelse med denne kompetence er “problem”, hvilket jeg vil gøre ved at diskutere det i forhold til begreberne ”opgave” og ”øvelse.”

Opgave, øvelse og problem

Opgave bruger jeg bredt som betegnelse for en eksplicit formuleret udfordring, til forskel fra udfordringer som ikke er eksplicit formulerede, og som derfor kun er en udfordring i kraft af nogens læsning af situationen. En opgave har således en objektiv karakter, forstået således at hvorvidt der er tale om en opgave eller ej ikke er afhængigt af, hvem der stiller den eller modtager den.

Ved et problem forstår jeg en situation der involverer en række metodeåbne spørgsmål der udfordrer en eller anden intellektuelt som ikke umiddelbart er i besiddelse af direkte metoder/procedurer/algoritmer der er tilstrækkelige til at besvare spørgsmålene (jf. Blum & Niss, 1991, s. 37). Et problem har således en subjektiv karakter i kraft af karakteristikkens understregning af at det drejer sig om noget der “udfordrer en eller anden”. Derfor medfører eksistensen af et problem også eksistensen af en eller flere personer det er et problem for.

En opgave kan for eksempel være “slå græsset” eller “find rødderne i andengradsligningen”. At skulle udføre et sådant stykke arbejde kan sagtens give anledning til forskellige problemer.

For eksempel kan græsslåmaskinen være gået i stykker eller man kan have mistet sin formelsamling eller man kan være på et for lavt uddannelses- eller erfaringsniveau (for et 8-årigt barn giver begge opgaver sandsynligvis anledning til problemer). Man kan altså stille alle en opgave, men ikke vide sig sikker på for hvem det er et problem.

For at kunne skelne klart mellem begreberne taler jeg om en øvelse, hvis det med rimelighed kan antages at en opgave ikke er eller vil føre til et problem for modtageren. I de tilfælde hvor løsningen af opgaven giver anledning til et problem for modtageren, vil jeg benytte termen “problem” i stedet for opgave. Opgave bliver derfor foreningsmængden af begreberne øvelse og problem, og jeg benytter termen opgave når modtagerens formåen ikke kan afgøres eller når opgavetypiseringen i øvelser og problemer ikke er i fokus.

Matematisk problemløsning

Problemløsning betegner simpelthen den proces hvorigennem man forsøger at løse et problem. Det helt centrale ved denne proces er at den – som “komplementærmængden” til arbejde med øvelser – er karakteriseret ved nødvendigheden af bevidste eller ubevidste metodemæssige overvejelser.

Matematisk problemløsning er så hvis det definerende ved processen – de metodemæssige overvejelser – involverer visse matematiske begreber, metoder og resultater.

I en matematikundervisningspraksis er det nemt at forestille sig betydelige overlap mellem situationer der udfordrer matematisk modelleringskompetence og matematisk problemløsningskompetence. “Kernen” i de to kompetencer er imidlertid forskellig, hvilket jeg nu vil udfolde nærmere ved at diskutere karakteren af hver type udfordring og relevansen af forskellige typer opgaver i den forbindelse.

Problemløsning og følelsen af fastlåsthed

Matematisk problemløsningskompetence handler om at håndtere en personlig oplevelse, hvis væsentligste karakteristika er frustration over at være kognitivt fastlåst – man ved ikke hvordan man skal få “hul på bylden” (jf. Blomhøj & Jensen, 2003, s. 127).

Som eksempel vil jeg stille dig som læser følgende opgave, lånt fra Schoenfeld (1985) som er en matematikdidaktisk klassiker og pionerudgivelse om matematisk problemløsning:

En vilkårlig trekant kan deles i to dele ved hjælp af et linjestykke parallelt med den ene side i trekanten. Hvordan skal linjestykket placeres så de to dele af trekanten bliver lige store?

Som læser af denne artikel er du sandsynligvis en der beskæftiger sig professionelt med matematikholdig undervisning, så jeg vil tro denne opgave opleves som et matematisk problem og derfor inviterer til matematisk problemløsning, fordi

• du i den konkrete situation godt forstår opgaven og har et klart billede af hvad udfordringen går ud,
• godt kan se, at der må eksistere en rimelig klart identificerbar løsning, men
• ikke umiddelbart ved, hvordan man skal nå frem til den.

Modellering og håndteringen af åbenhed

Matematisk modelleringskompetence handler om en arbejdsproces, hvis væsentligste karakteristika er behovet for forskellige former for afgrænsning og præcisering for at leve op til det definerende ved processen: At gøre en udfordring, der ikke som trekantopgaven ovenfor er ”født” i matematikkens univers, tilgængelig for matematisk repræsentation og bearbejdning. Afgrænsningsbehovet opstår ikke mindst i de indledende ”ydre” dele af modelleringsprocessen hvor der er rigtig meget andet end matematik i spil. Det svarer til de delprocesser der på figur 1 betegnes motivering og systematisering.

På grund af den ”underbestemte” karakter af disse meget åbne dele af modelleringsprocessen kan hovedudfordringen ofte beskrives som ”handlingslammelse grundet de mange forskellige veje man kan gå og fraværet af et udleveret kompas at navigere med” (jf. Blomhøj & Jensen, 2003, s. 127). Man skal håndtere de mange tilsyneladende lige meningsfulde valg der skal træffes før matematiske begreber og teknikker kan være til nogen nytte, kombineret med manglen på en veldefineret strategi for hvordan man træffer disse valg. Set gennem en didaktisk ”kompetencelinse” er matematisk modellering primært interessant som læringsaktivitet, hvis processen indebærer et sådant forsøg på håndtering af åbenhed (jf. Niss & Jensen, 2002, s. 52-53).

Her vil jeg bruge følgende opgave som eksempel:

Hvilken transportform er bedst?

Det er en opgave som jeg oplever som velegnet som invitation til at fx avu-kursister kan arbejde med alle dele af en matematisk modelleringsproces, men med tyngde på den indledende håndtering af åbenhed, fordi

• problemstillingen har en karakter, hvor man godt kan se for sig, at matematik kan være relevant at bringe i spil (tankegangskompetence),
• det er åbent, på hvilket grundlag man skal svare (hvad vælger man at lægge i ”bedst”?), hvorfor man selv skal træffe det valg (motivering),
• man derefter er nødt til selv at afgøre, hvilke forhold (fx centrale størrelser og deres indbyrdes forhold) man gennem modellen vil sætte fokus på, og hvilke man derved uundgåeligt kommer til at se bort fra (systematisering), og
• man på denne vis har givet sig selv muligheden for at arbejde med, hvordan de udvalgte forhold kan ”oversættes” til matematikkens sprog (matematisering).

Her kan man se et eksempel på, hvordan to kursister eksempelvis kunne gribe de indledende dele af denne proces an.

Her kan man se en række eksempler på opgaver som forfatteren af denne artikel har erfaring for er velegnede som invitationer til matematisk modellering. Her er frit slag for egen afprøvning af eksemplerne med afsæt i konstruktion af nye kursistdialoger fra klasserummet. Eksemplerne er kategoriseret med tanke på undervisningens tilrettelæggelse (jf. Jensen, 2007, s. 196): Den ene kategori er tænkt som oplæg til undersøgelser som kan bruges som inspiration ved etableringen af et projektarbejde, den anden kategori som oplæg til korterevarende opgaveløsning som kan fungere inden for rammerne af en undervisningslektion eller to.

Matematiseringskompetence

Her er et tredje konkret opgaveeksempel:

Hvordan afhænger den skat man betaler af indkomstskatte-procenten og moms-procenten?

Den er konstrueret som en invitation til at arbejde med matematisering, matematisk analyse og fortolkning, svarende til faserne (c)-(e) i en matematisk modelleringsproces (jf. figur 1). Motiveringen og systematiseringen af udfordringen er der allerede taget hånd om gennem formuleringen af opgaven, og tilbøjeligheden til at evaluere modelleringsprocessen i sin helhed (fase (f) i figur 1) kommer i vid udstrækning af selv at have arbejdet med de indledende afgrænsende dele af processen (jf. Jensen, 2007, s. 147-149). Opgaver af denne type, som man også kan få flere eksempler på ved at følge linket givet ovenfor, kan dermed ikke bruges til at udfordre alle dele af en matematisk modelleringsproces, men de kan udfordre en læringsmæssigt ofte helt afgørende del heraf: Anvendelsesorienteret matematisk problemløsning med fokus på matematisering (Ibid., s. 195-197).

Denne kombination vil jeg betegne matematiseringskompetence, som jeg vil karakterisere som nogens indsigtsfulde parathed til at løse problemer som opleves som sådan fordi de inviterer til matematisering.

Opgavemæssig udspænding af kompetencerne

Figur 2 er et bud på en sammenlignende didaktisk udspænding af matematisk modelleringskompetence og matematisk problemløsningskompetence, med afsæt i de begrebsdannelser og -forståelser jeg har fremlagt i denne artikel.

Figur 2. Eksempler på opgaver der kan bruges til en didaktisk udspænding af matematisk modelleringskompetence og matematisk problemløsningskompetence.

Kreditering

Artiklen er udarbejdet af Tomas Højgaard, lektor i matematikkens didaktik ved DPU - 2019, Aarhus Universitet.