Kompetenceorienteret matematikundervisning

Når de matematiske kompetencer skal tydeligt i spil i undervisningen, er første skridt at sætte dem klart og eksplicit på dagsordenen. Det kan ske ved i løbet af året at vælge nogle 2-4 uger lange forløb, hvor en udvalgt kompetence gøres til den styrende læringsmæssige ambition.

Artiklen her tager udgangspunkt i en sådan beslutning og giver konkrete eksempler fra indskoling, mellemtrin og udskoling med udgangspunkt i først symbolbehandlingskompetence, så ræsonnementskompetence.

1. Symbolbehandlingskompetence som sigtepunkt

I Fælles Mål er repræsentations- og symbolbehandlingskompetence beskrevet i samlet form. Denne artikel koncentrerer sig om sidstnævnte ud fra denne begrebsforståelse (jf. Blomhøj & Jensen, 2007, s. 30):

Matematisk symbolbehandlingskompetence betegner nogens indsigtsfulde parathed til både selv at gennemføre og forholde sig kritisk undersøgende til de former for handling, der består i at:

afkode symbol- og formelsprog,
oversætte frem og tilbage mellem symbolholdigt matematisk sprog og naturligt sprog,
behandle og betjene sig af symbolholdige udsagn og udtryk.

Denne karakteristik har den fordel, at den frigør kompetencen fra reference til et bestemt matematisk stof, hvorfor den samme grundforståelse kan bruges som udgangspunkt for forløb på alle klassetrin. Den er desuden brugbar som didaktisk værktøj, da den er kort formuleret som tre centrale forhold med hver deres ”huskeord” tilknyttet.

Herunder præsenteres tre eksempler med udgangspunkt i nedenstående tilrettelæggelsesmæssige udfordring:

I et forløb skal eleverne udvikle dels deres matematiske symbolbehandlingskompetence, dels deres forståelse af et centralt matematisk begreb, som kan rumme symbolbehandlingsmæssige udfordringer.

Til refleksion: Hvilke konkrete mål for elevers læring kan der formuleres og arbejdes frem mod? Hvilke aktiviteter og arbejdsformer understøtter opfyldelse af de formulerede mål for elevernes læring i forløbet?

1.1 Eksempel fra indskolingen

I indskolingen kan det centrale matematiske begreb være en af de fire regningsarter, fordi både regnetegnene og de tal, der opskrives og regnes med, typisk angives symbolsk. I et konkret forløb om subtraktion kan der formuleres disse mål for elevernes læring:

Eleverne udvikler deres forståelse af begrebet subtraktion i tilknytning til det at finde forskellen mellem to hele, positive tal, og deres færdighed i at finde resultatet af sådanne subtraktions-regnestykker.
Eleverne kan oversætte frem og tilbage mellem hverdagssprog og symbolsk sprog i forbindelse med det at finde forskelle mellem to størrelser givet i en konkret kontekst.
Elever kan afkode subtraktions-regnestykker i forhold til en konkret kontekst.

Aktivitetsmæssigt peger disse mål i retning af en kontekst, som inviterer til at finde parvise forskelle mellem forskellige heltallige størrelser. Med det udgangspunkt skal eleverne selv bygge enkle subtraktions-stykker, som de mener svarer til bestemte hverdagssproglige spørgsmål til konteksten (oversættelse). De skal også forholde sig til, om det kontekstmæssigt giver mening, når andre har bygget sådanne regnestykker (afkodning).

Arbejdsformerne knyttet til disse aktiviteter skal gerne få eleverne til at kommunikere med hinanden om det meningsfulde ved forskellige subtraktionsstykker i forhold til en given kontekst. Det kan ske ved at lade eleverne arbejde i makkerpar, hvor de på skift skal forklare, hvilket subtraktionsstykke, de mener, er det rigtige at bygge i forhold til en konkret kontekst-forskel. Herved kommer den ene til at arbejde med oversættelse til et symbolsk udtryk, mens den anden skal afkode, om det giver mening, jf. ovenstående mål for elevernes læring.

1.2 Eksempel fra mellemtrinnet

På mellemtrinnet kan der tages udgangspunkt i brøkbegrebet, fordi håndtering af symbolsk opskrivning af brøker som eksempelvis 3/4 udgør en central udfordring for mange elever. Målene for elevernes læring kan lyde således:

Eleverne udvikler deres forståelse af begrebet brøkdel i tilknytning til det at finde forholdet mellem to hele, positive tal.
Eleverne kan oversætte frem og tilbage mellem hverdagssprog og symbolsk sprog i forbindelse med det at finde forholdet mellem to størrelser givet i en konkret kontekst.
Elever kan afkode brøkdele i forhold til en konkret kontekst.

I forhold til aktiviteter og arbejdsformer peger disse mål naturligt nok i samme retning som indskolingseksemplet. Konkret kan eleverne arbejde med eksplicit formulerede oversættelses- og afkodningsopgaver med udgangspunkt i samme kontekst. Det kan være karakteristika ved de forskellige elever i en skoleklasse. Eleverne skal så ud fra konkrete oplysninger bygge brøker, som svarer til forskellige forhold formuleret i hverdagssprog, eksempelvis: Hvor stor en del af drengene har briller? De skal også finde kontekstmæssig mening til allerede opskrevne brøker.

1.3 Eksempel fra udskolingen

I udskolingen kan der anlægges et symbolbehandlingsfokus i forbindelse med arbejdet med formler, som pr. definition er symbolske udtryk. Det kan ske i et arbejde med såkaldte Fermi-problemer som; ”Hvor meget vand bruger du i løbet af en uge?” eller ”Hvor stor en del af jeres liv har I brugt på matematikundervisning?”, efter denne fremgangsmåde:

Vælg nogle variable, som I mener svaret afhænger af.
Byg en formel, som viser, hvordan man skal regne med disse variable.
Gæt kvalificeret på værdien af hver variabel.
Foretag beregninger med disse værdier ved at indsætte i formlen og beregne et cirka-svar på spørgsmålet.
Vurdér cirka-svaret: Virker det fornuftigt i forhold til spørgsmålet, eller skal beregningerne foretages på en anden måde?

Arbejdet med Fermi-problemer udvikler både elevernes symbolbehandlings- og modelleringskompetence. For et Fermi-forløb kan målene for elevernes læring derfor formuleres således:

Eleverne udvikler deres forståelse af, hvad en variabel er.
Eleverne kan gennemføre en bevidst systematisering af en problemstilling.
Eleverne kan bygge egne formler gennem indførelse af selvvalgte variable (oversættelse).
Eleverne kan forholde sig konstruktivt-kritisk til formler, som de selv eller andre har bygget (afkodning).

Det kan anbefales at søge på ”Fermi problems” for yderligere inspiration til arbejdet med denne metode.

Inspirationsvideoer

Der findes inspirationsvideoer i tilknytning til de forløb, der er omtalt her i artiklen. Nederst på siden findes link til en beskrivelse af hvert konkret gennemførte forløb og videoklip fra undervisningen.

2. Ræsonnementskompetence som sigtepunkt

Ved et ræsonnement forstås her den særlige måde at argumentere på, hvor man bruger fornuftsstyrede argumenter til at forbinde nogle konklusioner og de præmisser, som man mener ligger til grund herfor, jf. figur 1.

Figur 1. En visuel model af et ræsonnement

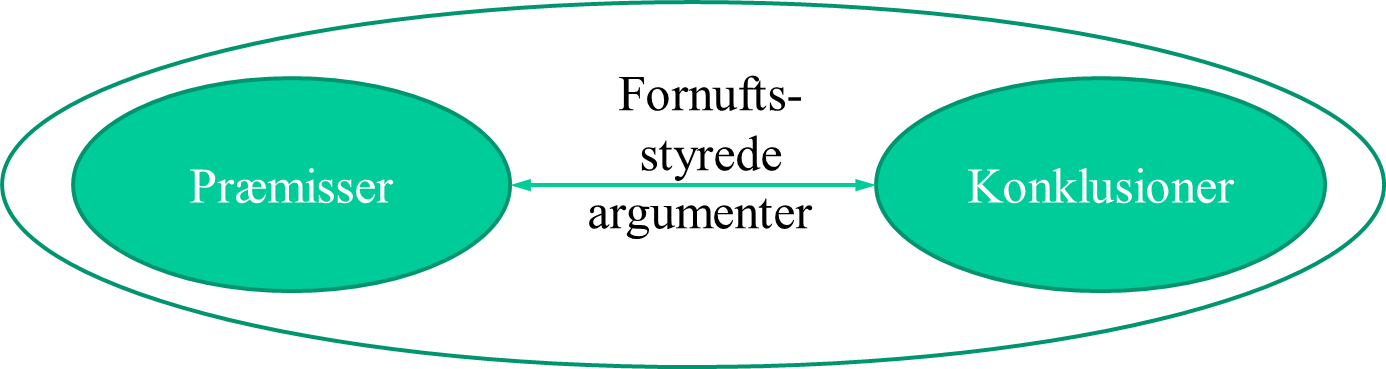
Med dette udgangspunkt arbejdes her med følgende forståelse af kompetencen - som i Fælles Mål er beskrevet sammen med tankegangskompetence:

Matematisk ræsonnementskompetence betegner nogens indsigtsfulde parathed til både selv at gennemføre og forholde sig kritisk undersøgende til ræsonnementer, hvor konklusionerne er matematiske.

Denne karakteristik frigør, ligesom karakteristikken af symbolbehandlingskompetence, kompetencen fra reference til et bestemt matematisk stof. Derfor kan den samme grundforståelse bruges som udgangspunkt for forløb på alle klassetrin. Desuden er karakteristikken kort og formuleret.

2.1 Eksempel fra indskolingen

I indskolingen kan eleverne arbejde med ræsonnementsorienterede opgaver i en geometrisk kontekst. Det gør det nemmere at knytte ræsonnementerne til noget visuelt, som eleverne både konkret og i tanken kan eksperimentere med. Disse mål for elevernes læring kan formuleres til et forløb om vinkler:

Eleverne udvikler deres forståelse af begrebet vinkel i tilknytning til simple geometriske figurer.
Eleverne kan argumentere for, om nogle givne vinkelmæssige karakteristika er mulige at opnå for forskellige simple geometriske figurer.

Aktivitetsmæssigt peger disse mål mod opgaver, som handler om vinkler i simple geometriske figurer, hvor det, der spørges til, inviterer til at svare med et argument frem for et konkret tal som følge af en måling eller beregning. Sådanne svar kan opnås med spørgemåder som disse: Forklar… Er det rigtigt, at…? Kan det lade sig gøre at…? Hvad er udgangspunktet (præmisserne), når du påstår, at…? Helt konkret kan eleverne få opgaver som:

Kan man tegne en trekant med:

tre spidse vinkler?
tre rette vinkler?
en stump og en ret vinkel?
en ret vinkel og to lige lange sider?

Arbejdsformerne knyttet til disse opgaver skal gøre det muligt og naturligt for eleverne at fremføre og forholde sig til hinandens argumenter. De kan arbejde i makkerpar og diskutere sig frem til en fælles besvarelse ved først at diskutere og gætte på, hvad hvert svar er, så prøve sig frem, i et dynamisk geometriprogram eller på ternet papir, og til sidst tegne og skrive deres endelige fælles svar og forklaring, så det kan fremlægges.

2.2 Eksempel fra mellemtrinnet

På mellemtrinnet kan der tilrettelægges et forløb, der kun har ræsonnementskompetence som læringsmæssigt sigtepunkt. Hvis forløbet skal bevidstgøre eleverne om, hvad et ræsonnement er, kan målene for elevernes læring formuleres således:

Eleverne udvikler bevidsthed om den rolle, præmisserne spiller, når man gennemfører ræsonnementer.
Eleverne kan gennemføre ræsonnementer som led i at håndtere konkret givne udfordringer.

Hvad angår arbejdsformen for denne form for ”rene” ræsonnementsforløb (eller modelleringsforløb, hvor det samme gør sig gældende), er det vigtigt, at eleverne kan arbejde nysgerrigt undersøgende med alle dele af kompetencen. Derfor kan sådanne forløb med fordel tilrettelægges som et projektarbejde, så eleverne i grupper får en sammenhængende periode, eksempelvis 2-3 uger, til dels at undersøge de ræsonnementsmæssige sider af noget, dels rapportere om deres undersøgelse ved at producere en tekst, en film eller lignende. I forløbet kan indlægges loops, hvor der kan evalueres ud fra tydelige delmål, om eleverne er på rette vej.

Aktivitetsmæssigt udvikles beherskelsen af den særlige form for arbejdsproces, som er karakteristisk for ræsonnementskompetence (og tilsvarende for modelleringskompetence) bedst, hvis eleverne får tid og rum til at arbejde med sådanne processer i deres helhed. Eleverne bør derfor få et overordnet spørgsmål, som de skal arbejde med de ræsonnementsmæssige sider af i hele projektperioden. Det kan handle om:

Sammenhængen mellem antallet af centicubes i en stang og stangens omkreds.
Hvordan man ved hjælp af programmering kan få noget bestemt til at ske.
Hvilke figurer der kan tesselere – og hvorfor.
Hvordan man laver en sudoku-opgave.

2.3 Eksempel fra udskolingen

I udskolingen kan der også planlægges forløb med ræsonnementskompetence som læringsmæssigt sigtepunkt. Arbejdsformen vil også her med fordel kunne være problemorienteret projektarbejde.

Aktivitetsmæssigt kan to former for progression tænkes ind i elevernes arbejde med at udvikle ræsonnementskompetence. Den ene handler om i stigende grad at hjælpe de forskellige elevgrupper med selv at vælge og formulere et relevant udgangspunkt for deres ræsonnementsmæssige undersøgelse. Det udvikler autonomi i kompetenceudøvelsen og opleves af mange elever motiverende, men det udfordrer også deres evne til at fastholde et ræsonnementsfokus i deres undersøgelse. Derfor er det en god ide at bevidstgøre eleverne om, hvad et ræsonnement er. Det kan ske for eksempel med udgangspunkt i en samtale om forskellen på påstande og argumenter fulgt op af fælles arbejde med figur 1.

Den anden form for progression handler om at sigte efter den side af ræsonnementskompetence, som handler om at forholde sig kritisk til andres brug af ræsonnementer. Det kan ske med afsæt i følgende mål for elevernes læring:

Eleverne har viden om ræsonnementers grundstruktur.
Eleverne kan bruge denne viden til at forholde sig kritisk undersøgende til andres brug af ræsonnementer.

Inspirationsvideoer

3. Inspiration og forslag til fagteamet

Det kan i tilrettelæggelsen af kompetenceorienterede forløb være nødvendigt at konkretisere målene for elevernes læring, så de kan bygge bro mellem de overordnede mål for forløbet i årsplanen og det konkrete valg af elevaktiviteter og arbejdsformer. En konkretisering udfordrer forståelsen af det overordnede kompetencemål.

I små videoer om hvert kompetencemål findes inspiration og input, der kan anvendes i fagteamet i forbindelse med konkretisering af det overordnede kompetencemål. Videoerne er udarbejdet i forbindelse med et udviklingsforløb i Ishøj Kommune.

Find videoerne her: Kompetencebaseret matematikundervisning

Der findes også inspirationsvideoer i tilknytning til de forløb, der er omtalt her i artiklen. Alle forløb har været gennemført i forbindelse med forskellige forsknings- og udviklingsprojekter. Nedenfor findes link til en beskrivelse af hvert konkret gennemførte forløb og videoklip fra undervisningen.

Symbolbehandlingskompetence som sigtepunkt

Find eksempler på forløb på matematikdidaktik.dk

Ræsonnementskompetence som sigtepunkt

Find eksempler på forløb på matematikdidaktik.dk

Læs også om kompetenceorienteret matematikundervisning i faghæftet for matematik, som du finder her: Læseplan og vejledning

Kreditering

Artiklen er udarbejdet af Tomas Højgaard, lektor i matematikkens didaktik ved DPU, Aarhus Universitet.

Artikel