Artikel
Sådan kan du arbejde med modellering
Modellering handler om at bruge matematikken til at forklare og besvare problemstillinger fra den virkelige verden.
Denne artikel giver et bud på, hvordan undervisningen, med modelleringskompetencen i fokus, kan struktureres. Artiklen kommer desuden med et konkret forslag til et forløb på A-niveau, hvor modelleringsprocessen gennemføres.
Hvad betyder modellering i matematik?
På alle tre gymnasiale niveauer består modelleringskompetencen i på den ene side at kunne analysere grundlaget for og egenskaberne ved foreliggende modeller og at kunne bedømme deres rækkevidde og holdbarhed. Hertil hører at kunne afkode og fortolke modelelementer og resultater i forhold til den situation, som er modelleret.
På den anden side består kompetencen i at kunne udføre aktiv modelbygning i en given sammenhæng, dvs. at bringe matematik i spil og anvendelse til behandling af anliggender uden for matematikken selv.
Aktiv modelbygning indeholder en række forskellige elementer:
- Først at kunne strukturere det felt eller den situation, der skal modelleres.
- Dernæst at kunne gennemføre en matematisering heraf, dvs. en oversættelse af objekter, relationer, problemstillinger så der kan laves en matematisk model.
- At kunne behandle den udarbejdede model, herunder løse de matematiske problemer den måtte give anledning til,
- At kunne validere den færdige model, dvs. bedømme dens holdbarhed både internt (i forhold til modellens matematiske egenskaber) og eksternt (dvs. i forhold til det felt og den situation, modellen omhandler).
- At kunne analysere modellen kritisk, både i forhold til dens egen brugbarhed og relevans og i forhold til mulige alternative modeller, og at kunne kommunikere med andre om modellen og dens resultater.
Modellering er altså en matematisk aktivitet, der forsimplet kan siges at indeholde tre aspekter; en situation eller problemstilling fra den virkelige verden, en bevægelse til den matematiske verden, og endelig en fortolkning tilbage til den virkelige verden.
Tomas Højgaard Jensen præsenterer i Udvikling af matematisk modelleringskompetence som matematikundervisningens omdrejningspunkt – hvorfor ikke? nedenstående model, der udpeger de enkelte faser i modelleringen, så de fremstår tydeligere og bedre kan bruges til planlægning af den praktiske undervisning.
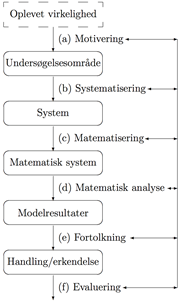
Her er ikke tale om en færdig opskrift til modellering, men en abstrakt konstruktion af faser, der kan være mere eller mindre bevidst til stede under konstruktion af en matematisk model. Disse faser gennemløbes ikke nødvendigvis i den opstillede rækkefølge, ligesom man i processen ofte vil springe frem og tilbage mellem faserne.
Planlægning
Det vil være en god idé at overveje i sin årsplanlægning, hvor og i hvilke forløb man sammen med eleverne arbejder med modellering. En mulighed er at gøre det i ét længerevarende forløb, men det kan også være praktisk at inddrage de enkelte faser under forskellige faglige emner, og til sidst afslutte med et projekt, hvor det hele kobles sammen.
Eksempler
I bilaget findes eksempler på, hvilke typer af spørgsmål man kan stille eleverne i de enkelte faser. Derudover er der forslag til en række emner som kan bruges til både kortere og længerevarende forløb.
Øvelsen ”To fjer til fem høns – matematisk rygtespredning”, er en aktiv måde at introducere eleverne til modellering. Her er tanken, at eleverne gennem den praktiske øvelse motiveres til at opstille en matematisk model til at beskrive situationen. Herved opdager de, at en eksponentiel funktion kun i begrænset omfang kan beskrive væksten korrekt, og at de derfor må finde en mere passende beskrivelse af situationen gennem logistisk vækst.
Kreditering
Peter Christiansen, Niels Brock Innovationsgymnasium
Materialet er udarbejdet af Centre for Undervisningsmidler (CFU) - en del af af Danmarks Professionshøjskoler.

Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.


