Forløb
Forløb om kviklån og lånetilbud
Forløb om annuitetsregning og lån på nettet og om at udarbejde lånetilbud på en bil. Henvendt til matematik på C-niveau.
Del 1: Eksempel 1 på lån på nettet
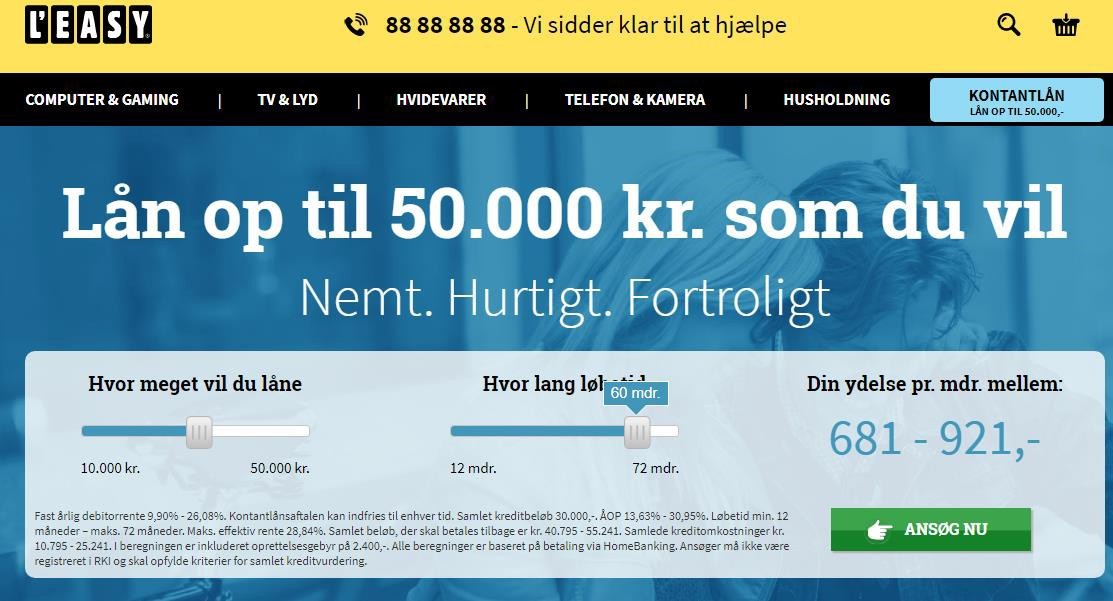
Annoncen fra L’EASY oplyser at man kan låne 30 000 kr. og betale tilbage over 60 måneder (5 år). Ifølge annoncen bliver den månedlige ydelse mellem 681 kr. og 921 kr.
1a) Bestem den årlige rente der er ved månedlig ydelse på 681 kr., og bestem den årlige rente der er ved månedlig ydelse på 921 kr.
1b) Hvad er forskellen på de samlede renteudgifter i kroner og øre i de to tilfælde?
Del 2: Eksempel 2 på lån på nettet
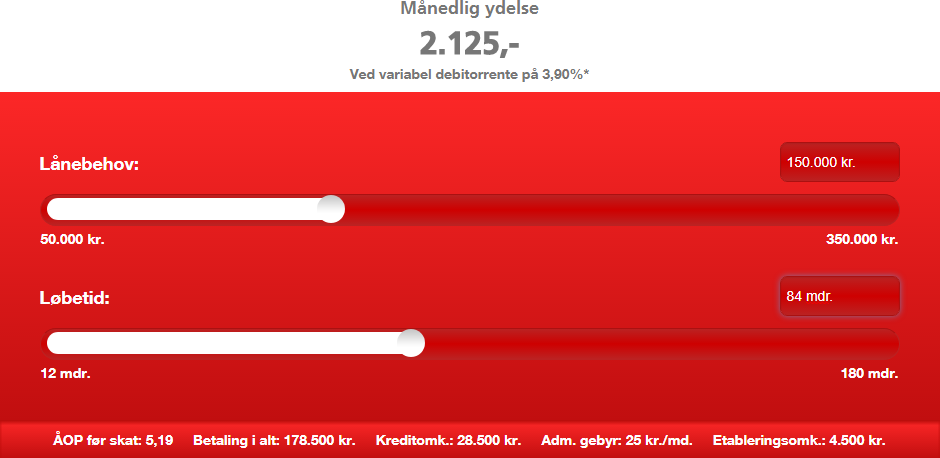
Annonce på internettet fra Santander Consumer Bank:
2a) Regn efter om alle oplysninger i annoncen er korrekte.
2b) Annoncen oplyser administrationsgebyr og etableringsomkostninger. Diskuter hvordan disse udgifter skal indgå i beregningerne af omkostninger ved lån og ved ÅOP (dvs. ’årlige omkostninger i procent’).
2c) Vurder ved hjælp af udregninger om den opgivne ÅOP kan passe.
Det kan være vanskeligt at udregne ÅOP eksakt, men I kan fx skitsere hvordan man vil kunne udregne den og prøve jer frem.
2d) Hvilken indvirkning på jeres beregninger har det at rente (i annoncen benævnt ’debitorrenten’) er variabel? Hvad vil der ske hvis renten stiger eller falder?
Del 3: Udarbejd tilbud på lån
Hanne Sørensen ønsker at låne 350 000 kr. til en ny bil. Hun vil tilbagebetale over højst 10 år med månedlige afdrag.
3a) Udarbejd mindst to forskellige tilbud til Hanne Sørensen.
I begge tilbud skal følgende gælde:
- der skal indgå realistiske, men forskellige renter
- der skal indgå månedlige afbetalinger og rentetilskrivninger
- de to tilbud skal have forskellige løbetider
- i tilbuddene skal de samlede udgifter til lånene fremgå.

Kommentar til læreren
Om eleverne/kursisterne vælger at udregne vha. formel eller regneark, kan afhænge af hvordan stoffet er gennemarbejdet i et konkret forløb – begge dele er muligt her.
Hvis elever arbejder i TI Nspire, kan der opstå udfordringer med at bestemme r vha. solve, særligt hvis n er stor. Man kan hjælpe ved at skrive intervalgrænser for r.
Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.


