Artikel
Inspiration til hvordan man arbejder med demokratisk dannelse i faget matematik på avu og FVU
FVU og avu matematik skal bidrage til at styrke voksnes deltagelse i det formelle og levede demokrati. Artiklen gennemgår spørgsmål som matematiklærere skal overveje i planlægning af undervisning, og giver nogle eksempler.
Formålene med FVU og avu matematik
Demokratisk dannelse indgår i formålene med FVU og avu matematik:
- FVU Stk. 1 : ”… styrke deres forudsætninger for aktiv medvirken i alle sider af samfundslivet.”
- Avu Stk. 3 : ”Undervisningen bygger på åndsfrihed, ligeværd og demokrati. Undervisningen tilrettelægges, så kursisterne styrker deres forudsætninger for aktiv medvirken i et demokratisk samfund.”
Kompetence, vilje og mod på matematik har betydning for voksnes aktive medborgerskab, da tal, diagrammer og beregninger indgår meget bredt:
• både i politiske og administrative overvejelser og beslutninger
• og i borgernes overvejelser og beslutninger i hverdagen
De danske demokratitænkere Alf Ross (1946a,b) og Hal Koch (1945) talte dels om det repræsentative demokrati med stemmeret og andre rettigheder, og dels om det levede demokrati med samtale og vilje til samforståelse.
Det repræsentative demokrati og matematikundervisningen
Det repræsentative/formelle demokrati er en styreform, og retfærdighed og effektivitet kan have matematiske begrundelser: Skovsmose (1994) kalder det for matematikkens formatterende kraft.
Lærere bør i planlægning af undervisning overveje: Hvordan kan vi motivere til og arbejde med matematiske algoritmer i det aktuelle danske valgsystem? Øger det deltageres/kursisters forståelse af matematikkens betydning at A) sammenligne forskellige optællingsalgoritmer ved kommunalvalg eller at B) sammenligne danske folketingsvalg med andre lande og andre historiske perioder?
Se mere om geografiske og historiske sammenligninger i artilen "Sådan kan du motivere og gøre matematik anvendelig med basale aktiviteter" også her på emu.dk.
Eksempel 1:
Deltagere/kursister kan bruge forskellige algoritmer til at tælle stemmer op, f.eks. stemmer fra det seneste kommunalvalg i jeres kommune. Forholdsmæssig/proportionalitet, Sainte-Laguës, D’Hondts.
Hvilken metode synes I er mest retfærdig?
Sainte-Laguës fordelingsmetode | lex.dk Den Store Danske D'Hondts metode
Wikipedia, den frie encyklopædi
Eksempel 2:
Deltagere/kursister kan behandle stemmerne til det danske folketingsvalg i 2019 med metoden ’flertalsvalg i enkeltmandskredse’ fra f.eks. USA og Storbritannien. Brug f.eks. storkredse som enkeltmandskredse. Sammenlign så med, hvordan Folketinget blev sammensat efter valget i 2019 efter den danske regel om proportionalitet. Deltagere/kursister kan også deltage i fortolkningen af lærerens eller andres omregninger, og dernæst diskutere retfærdighedskriterier, fx ud fra figur 1 og 2:
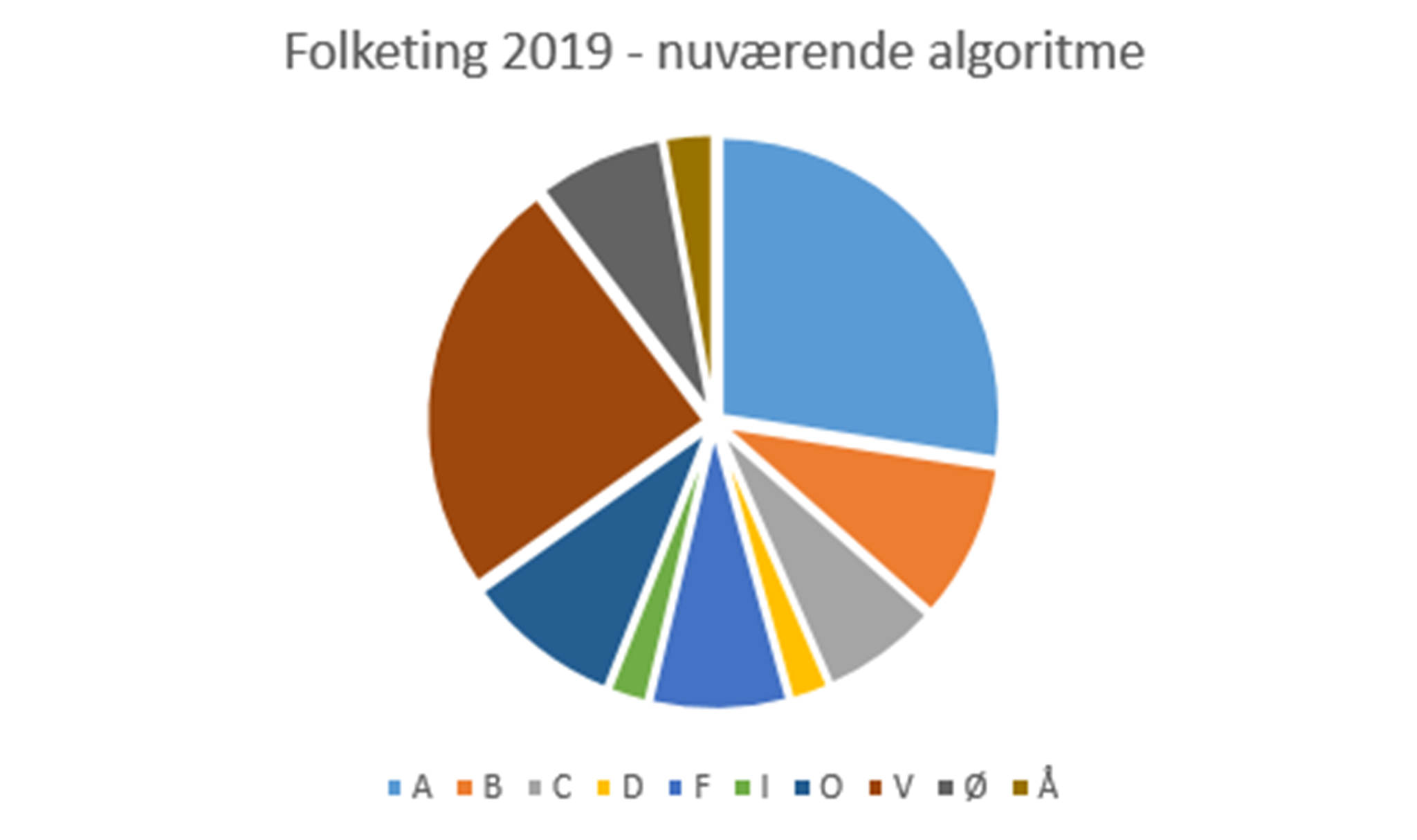
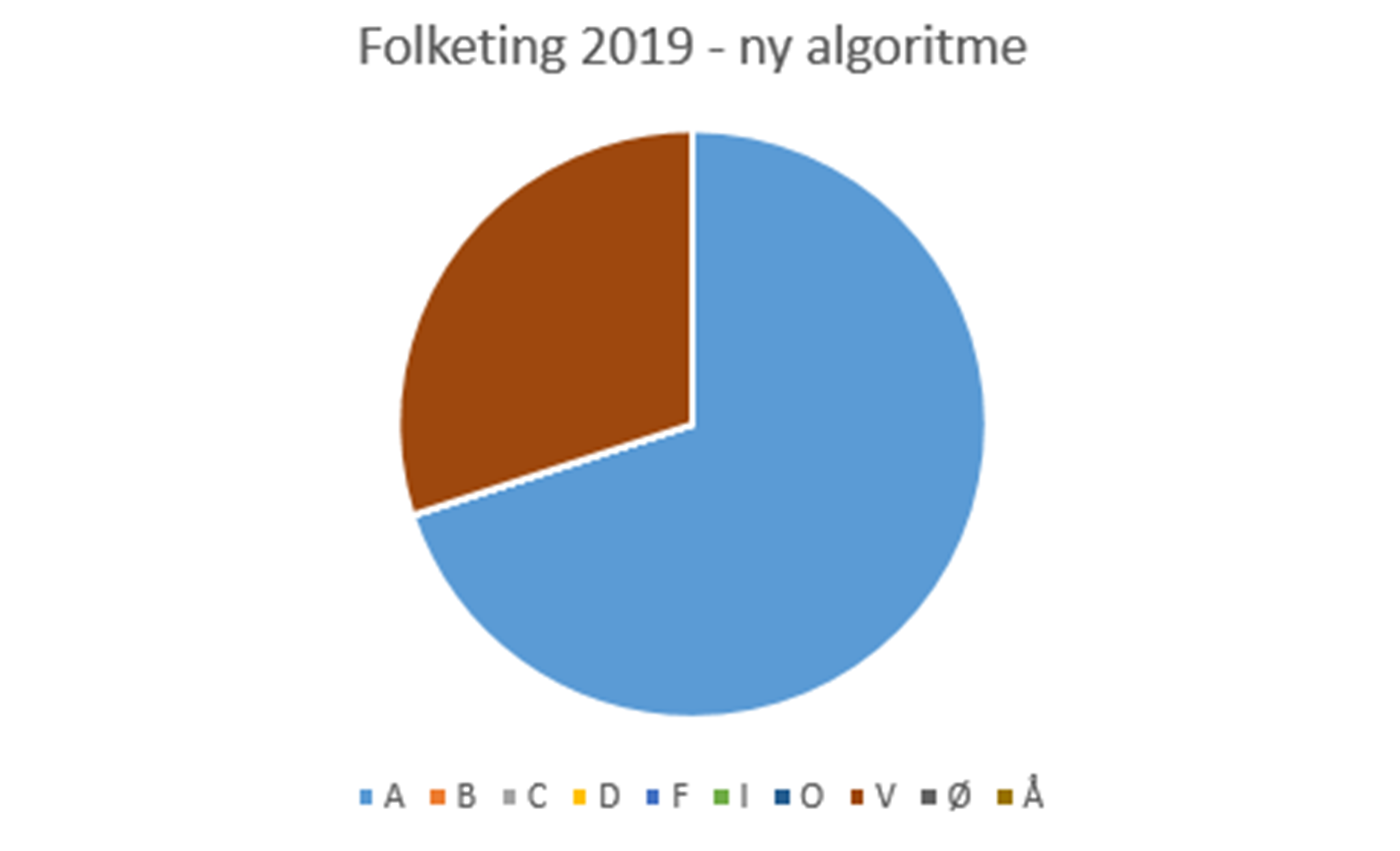
Eksempel 3:
Deltagere /kursister kan opsøge, bearbejde og formidle data om befolkningsgruppers brug af stemmeret og andre indflydelsesveje.
Det repræsentative/formelle demokrati i Danmark handler også om lighed til uddannelse
Lærere bør overveje:
- Har der været og er der demokratisk ligeret til matematisk uddannelse?
- Til FVU-matematik? Til avu-matematik?
- I alle dele af Danmark?
- Hvor mange forlader i dag folkeskolen uden at have de nødvendige matematiske kompetencer?
- Er dette tal steget eller faldet de sidste fx 20 år? Hvilke matematiske kompetencer er for den almindelige borger nødvendige for at kunne deltage i det repræsentative og levede demokrati?
- Hvordan minimerer man matematik-frygt og matematik-angst?
Det levede demokrati og matematikundervisningen
Det levede demokrati eller hverdagsdemokratiet er en måde at leve på. Demokratiske samtaler og dialoger er værdifulde i sig selv. De kvalificerer beslutningsprocesser og udvikler og danner mennesker. Matematik og matematiske begreber indgår ofte i offentlige, demokratiske debatter, udtalelser, påstande og samtaler. I nogle tilfælde indgår beregninger og matematiske modeller som grundlag for dispositioner og beslutninger. Det bør matematikundervisningen for voksne inddrage eksempler på og bearbejde. Se fx Lindenskov (2004) om, hvorfor og hvordan man kan bruge offentlige medier i undervisningen.
Lærere kan overveje:
I hvilke eksempler i den aktuelle mediedækning indgår eller kunne der indgå matematik, der matcher indholdet i FVU og avu-matematik? Hvilke kontekster kan være motiverende for de voksne at arbejde med?
Eksempel 4:
Brug klip fra medierne som grundlag for deltageres/kursisters arbejde med at formulere og behandle matematiske spørgsmål. De voksne kan også selv finde og behandle grunddata og resultater i medierne. De kan fx nyberegne og videreberegne, og de kan illustrere resultater på alternative måder afhængigt af deres matematiske viden og kompetence.
Eksempel 5:
Deltagere/kursister kan også deltage i at sammenligne forskellige mediers matematiske formidling af det samme emne.
Det levede demokrati foregår i større eller mindre grad i selve matematikundervisningen. Matematikundervisning, hvor bogen eller læreren stiller spørgsmål og opgaver og afgør om deltagernes spørgsmål og svar er relevante, er en autoritær undervisning. Den socialiserer til lydighed og underdanighed, og det kan skade deltagernes forudsætninger for at indgå i det levede demokrati uden for skolen. Omvendt kan matematikundervisning med demokratiske læreprocesser styrke disse forudsætningerne. Se redskab til Pulsmåling af hverdagsdemokratiet i Demokrati og aktivt medborgerskab | emu danmarks læringsportal
Lærerne bør i planlægning af undervisning overveje:
Hvilke muligheder for demokratiske læreprocesser og dermed de voksnes indflydelse, giver indhold og undervisningsformer mulighed for? Giver undervisningen mulighed for, at deltagerne kan opleve matematik som meningsfuldt? Er der ytringsfrihed, ligeværd og tolerance i gruppe- og klassediskussioner, og i de voksnes fremlæggelser for hinanden?
Paul la Cour var på Askov Højskole en af de første i Danmark, der underviste voksne i matematik. Matematik var nemlig nødvendig som hjælpefag for naturvidenskaben og den teknologi, som var relevant for den voksne landbefolkning. Med sine matematikbøger ønskede la Cour, at de voksne fik matematisk forståelse ved at give dem mulighed for at tale ud fra egne forståelser og med egne ord. la Cour ønskede, at de voksne kom til at sætte pris på matematik og dermed kom til at føle sig berigede. Disse formuleringer fra omkring 1900 er stadig inspirerende!
Når deltagere/kursister inviteres til at øve indflydelse på temaer og kontekster for matematikundervisningen, kan der opstå dilemmaer. Skal deltagere/kursister vælge den kontekst, der umiddelbart synes mest relevant? Eller skal de vælge ud fra hvilket matematisk indhold, der kan motivere og udfordre dem mest? Det sidste kræver, at læreren kan formulere, hvad det konkrete matematiske arbejde kommer til at indeholde. Se et eksempel på dette dilemma fra et avu-hold (Hansen & Lindenskov, 2004).
Omvendt er det uden dilemmaer at give deltagere/kursister mulighed for indflydelse på evalueringen af, om deres svar på matematikopgaver er rigtige. I et tværnationalt projektsamarbejde mellem voksenundervisningscentre om matematikundervisning fortalte nogle af kursisterne, at de fik deres bedste oplevelse i projektet var, da de fik redskaber til selv at kunne afgøre, om et svar var korrekt, fx ved at kunne kontrollere en multiplikation ved at udføre en division, og fx ved at lære noget om overslagsberegning. Det var frisættende, fortalte de, at de ikke altid var nødt til at bede læreren kontrollere, men kunne gøre det selv. (van Groenenstein, Lindenskov, 2004).
Tre hensigter
Nogle forskere (Navarro-Medina & de-Alba-Fernandez 2015, s. 46) deler hensigten med undervisning, der omfatter demokratiske aspekter, op i 3 dele:
- at styrke deltagerens viden om demokratiets lovgrundlag og offentlige praksis
- at styrke deltagernes personlige og moralske dannelse, herunder deres identitet og indstilling
- at lade deltagerne få praktisk erfaring med at deltage demokratisk i og uden for klasseværelset
For matematikundervisningen betyder det fokus på:
- at deltagere/kursister oparbejder relevant viden og matematisk kompetence til at forstå og forholde sig til matematikkens roller i både det formelle og det levede demokrati
- at de oparbejder matematikfaglig selvtillid i forhold til det formelle og det levede demokrati
- at deltagerne får erfaring med at behandle og anvende matematik i demokratiske situationer i og uden for klasseværelset
Både det kognitive med viden og kompetence og det affektive med selvtillid og mod skal således være i fokus.
Refleksion og udvikling af matematikundervisningens demokratiske former og funktioner.
De nævnte spørgsmål som lærere kan overveje kan sammen med en afprøvning af eksempler støtte refleksion om og udvikling af matematikundervisningens demokratiske former og funktioner. Det kan ske,
- på læreruddannelse og efteruddannelse
- når lærerne individuelt og sammen med deltagere/kursister overvejer, i hvilke sammenhænge deres matematikundervisning behandler og opfylder formålet om demokratisk medborgerskab, samt i hvilke sammenhænge den virker begrænsende
- når matematiklærerne sammen på et eller flere uddannelsessteder tager pulsen på deres matematikundervisning samt inspirerer hinanden
omvedrørende indhold og undervisningsmetoder til brug i efterfølgende forløb.
Inspiration til andre faglærere
Som nævnt har matematik en særlig formatterende funktion i samfundets indretning og virkemåde (Skovsmose, 1994). På trods af det kan også andre fags lærere finde inspiration fra de nævnte spørgsmål til overvejelse og fra eksemplerne.
Kreditering
Lena Lindenskov, Lektor, ph.d., matematikkens didaktik, Afdeling for Fagdidaktik, DPU – Aarhus Universitet - 2021
- Groenestijn, M. van & Lindenskov, L. (Eds). Mathematics in Action, Communalities across Differences, a handbook for teachers in adult education. Netherlands: Publisher ALL Foundation.
- Koch, H. (1945/1991). Hvad er demokrati? 5. udg. København: Gyldendal.
- la Cour, P. (1898, 1898, 1899). Historisk matematik: Et indledende kursus, Bind 1–3. Det Nordiske Forlag.
- Lindenskov, L. (2020). Didaktisk model for matematikundervisning og demokrati. I: C. Haas; C. Matthiesen (red). Fagdidaktik og demokrati. Frederiksberg: Samfundslitteratur, s. 29-50.
- Lindenskov, L. (2019). Sådan kan du motivere og gøre matematik anvendelig med basale aktiviteter. emu danmarks læringsportal
- Lindenskov, L., Hansen, E.P. (2004). Two Dilemmas in Communicating Mathematics in Adult Basic Courses: "How to Support Pre-Knowledge of Adult Learners" and "How To Support Democratic Classroom Decisions." 29-33. Proceedings of the International Conference on Adults Learning Mathematics 7, 2000 alm-00-proceedingsalm07.pdf (alm-online.net)
- Lindenskov, L., (2004). Aviser i matematikundervisningen – hvorfor og hvordan? - matematisk opmærksomhed med og mod avisen som medie. LAMIS Sommerkurs Matematikk i Livet - 2003, Trondheim: NTNU-trykk, s. 58 – 82. ISBN 82-471-6014-5.
- Navarro-Medina, E. & de-Alba-Fernandez, N. (2015). Citizenship education in the European curricula. Procedia – Social and Behavioral Sciences, 197: 45-49.
- Ross, A. (1946a/1967). Hvorfor demokrati? 2. udg. København: Nyt Nordisk Forlag.
- Ross, A. (1946b): Anmeldelse af 'Ordet eller Sværdet?', Politiken, 23. marts. Alf Ross: Anmeldelse af 'Ordet eller Sværdet?', 23. marts 1946 (danmarkshistorien.dk)
- Skovsmose, O. (1994). Towards a philosophy of critical mathematics education. Dordrecht: Klüwer Academic Publishers.
- VIA, KP, Dansk Flygtningehjælp & Als Research (2019). Demokrati og aktivt medborgerskab. emu danmarks læringsportal
Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.


