Forløb
Undersøgende forløb - Cairoflisen
Her præsenteres et forløb, hvor den undersøgende tilgang til en problemstilling i matematik er i fokus.
Indledningsvis udfolder artiklen begreberne åben og undersøgende matematikundervisning. Herefter præsenteres forløbet Carioflisen, hvor den fagdidaktiske tilgang bliver eksemplificeret.
Bilagene til artiklen indeholder forslag til elevoplæg og modeller af cairoflisen til fremstilling eller kopi.
Cairoflisen - en undersøgende aktivitet i matematik
”Bevidstheden om, at matematikken er en model af virkelighedens opgave, og ikke nødvendigvis en helt præcis model må derfor være genstand for undervisningen, og eleverne må udover selve beregningerne trænes i at arbejde med det autentiske materiale, oversættelsen til modellen, og oversættelsen tilbage til virkelighedens opgave med en vurdering af resultatet.”
Ovenstående citat er hentet fra ”Vejledning til Grundfagsbekendtgørelsen i matematik i erhvervsuddannelserne”, og det er med dette udgangspunkt, artiklen her udfolder begrebet undersøgende matematikundervisning i praksis - her eksemplificeret med et undervisningsforløb: Cairoflisen.
Åben, undersøgende og eksperimenterende!?
De tre ord anvendes ofte i forbindelse med arbejdet i matematik med en undersøgende tilgang. Der er ingen fastdefineret, entydig definition på de begreber, når de anvendes i forbindelse med matematikundervisningen. I denne artikel anvendes åben som signal til, at opgaveformuleringen overlader nogle beslutninger til de elever, der skal løse opgaven. Undersøgende og eksperimenterende indikerer, at der er flere måder at arbejde med problemstillingen på, og at den første løsning måske ikke automatisk er den bedste.
Undersøgende matematikundervisning i praksis
I tilrettelæggelsen af et undersøgende undervisningsforløb kan en trefaset struktur være en stor hjælp for lærerens tilrettelæggelse og gennemførsel af forløbet:
(1) Iscenesættelsen, (2) Elevernes undersøgende arbejde og (3) Fælles refleksion og faglige pointer.
(1) Iscenesættelsen
Det er en kompetence at kunne handle med overblik i sammensatte situationer med matematik. For at give eleverne mulighed for at mestre den kompetence må den enkelte opgave præsenteres i en kontekst, så det er eleverne, der får udfordringen til og fornøjelsen af at være dem, der afgrænser og formulerer problemer, opsøger information, stiller spørgsmål, danner hypoteser, opstiller modeller samt diskuterer med hinanden og læreren.
Det stiller krav til læreren, der via en opgaveformulering sætter scenen for undervisningen.
Iscenesættelsen bør være andet end en gold opgave på A4-papir.
I Matematikmorgener (2006) består iscenesættelsen af et brev til eleverne med ønsker og krav til form og indhold og i Farlige små tal (2006), der handler om risikoen for at få æg med salmonella, indgår en indkøbsvogn med 500 fotohylstre med gule eller blå centicubes som blommer i iscenesættelsen. I artiklen her med den aktuelle opgave præsenteres mulige iscenesættelser på Bilag 2 og 3.
En god iscenesættelse skaber motivation hos dem, der skal arbejde med den undersøgende problemstilling, og læreren får skabt et rum for dialogisk samspil i klassen ved at stille åbne og nysgerrige spørgsmål, inspirere og støtte, udbygge og sammenkæde elevernes erfaringer, samt fastholde dem i systematiske undersøgelser.
(2) Elevernes selvstændige og undersøgende arbejde
At arbejde undersøgende kræver tid, frihed og støtte til at kunne etablere et samarbejde, hvor eleverne kan arbejde selvstændigt med problemet. Det betyder ikke, at eleverne er overladt til sig selv i arbejdsprocessen - tværtimod kræver den undersøgende arbejdsform både lærerstøtte og dialog mellem deltagerne.
I Trenger en å spørre for at være spørrende (2012) diskuterer forfatterne, hvad det kan betyde at være undersøgende og spørgende i læringssamtaler i klassen i matematik.
Her argumenteres for at anvende spørgende udsagn, fx ” Kunne det tænkes….”, ”Hvad nu hvis….?” og ”Hvordan kan det være, at….?.
Spørgende udsagn er tentative - de er dvælende, nølende og udforskende.
(3) Fælles refleksion og faglige pointer
Det undersøgende arbejde indebærer opbygning af en fælles faglig viden med et fælles fagsprog, der kan medvirke til etablering af forbindelser til tidligere erfaringer og etableret viden. Erfaringerne fra det undersøgende arbejde og resultater og refleksioner fra forløbet skal systematiseres og gøres fælles, men erfaringerne viser også, at det er det punkt, der bruges mindst tid og opmærksomhed på.
Læreren bør derfor tage ansvar for, at de faglige pointer, der er indeholdt i det undersøgende arbejde, bringes op i fællesskabet. Det kan dels gøres på baggrund af de observationer, læreren har foretaget under forløbet og dels med udgangspunkt i de elevfremstillede besvarelser og produkter.
Eleverne kan præsentere deres løsningsforslag for hinanden med fokus på de faglige pointer i par, i grupper, i plenum eller på en digital platform, som fx en padlet. De kan også formulere oplæg med opgaver til hinanden med udgangspunkt i det lærte.
Fire kategorier af tilgange til konstruktion af undersøgende opgaver og oplæg
En matematikopgave med undersøgende potentiale anskues her med fire forskellige tilgange:
Et rent matematisk indhold, et tematisk indhold, en modelleringssituation og en autentisk modellering med kritisk potentiale.
1. Rent matematisk
Det centrale er her at fokusere på det, der skal læres – og finde den rette undersøgende situation, som kan bringe det konkrete matematiske begreb i spil.
Eksempler kan være arbejde med trekanter og trekantuligheden, fx med et reb som hjælpemidlet eller rumfang, hvor opgaven for en VVS’er kan være at designe en kop som en cylinder, der kan indeholde præcis ¾ liter.
2. Tematisk
Genstanden for undersøgelsen kan være et tema, fx Matematikmorgener (2006), hvor der undersøges hvilken matematik, der kan være indeholdt i en morgen - fra eleven vågner helt frem til, at undervisningen begynder, eller hvordan en grillstarter, som smeden skal designe, skal se ud.
Her er det temaet, der er i fokus, og så skal forskellige matematiske discipliner bidrage med at beskrive det.
3. Modelleringssituation
Her er autenticiteten helt central. Det, der skal undersøges, skal have helt reel omverdens-karakter, og det skal kunne undersøges med matematik.
Eksempler her kan være en undersøgelse af hvor mange mursten, der er behov for til en mur, om et værelse skal males eller tapetseres, eller hvad det koster at tage på job med forskellige transportformer.
I ”Vejledning til Grundfagsbekendtgørelsen i matematik i erhvervsuddannelserne” beskrives modelleringskompetencen som at være noget helt centralt i matematikundervisningen:
”I erhvervsuddannelserne spiller kompetencerne forskellige roller og har forskellig vægtning på de fire niveauer. På niveau F og E er matematisk modellering den centrale kompetence – evnen til at kunne bruge matematikken som model til at løse opgaver fra erhvervene, samfundet og privatlivet. De øvrige kompetencer er også målsatte, men som bidrag til matematisk modellering. For at kunne anvende matematikken som model, er det helt centralt at kunne tænke matematisk om praktiske udfordringer (tankegang) og at kunne håndtere de tal, formler og symboler, som bruges i matematikkens beskrivelse af forhold i erhvervene og i hverdagen (symbol og formalisme). Det er ligeledes nødvendigt at kunne kommunikere om sine løsninger (kommunikation) og at bruge de hjælpemidler, som er passende i situationen (hjælpemiddel).”
4. Autentisk modelleringssituation med kritisk potentiale
Her giver anvendelsen af matematik anledning til at diskutere modellerne ud fra bestemte holdninger og indse, at matematik kan bruges med bestemte formål. Derigennem har matematikken et kritisk potentiale.
Eksempler kan være en undersøgelse om, fx hvorvidt det kan betale sig for eleverne at forsikre deres cykler sammen eller om sammenhængen mellem udviklingen af lærlingeløn og de erfaringer, eleverne opnår, er rimelig og er der rimelighed i den forskellige startløn mellem erhvervene?
I alle disse fire beskrevne tilfælde er det selvfølgelig vigtigt for elevernes motivation, at målet med aktiviteten er klart - at de er helt klar over, hvad er det er for en matematik, der skal læres!?
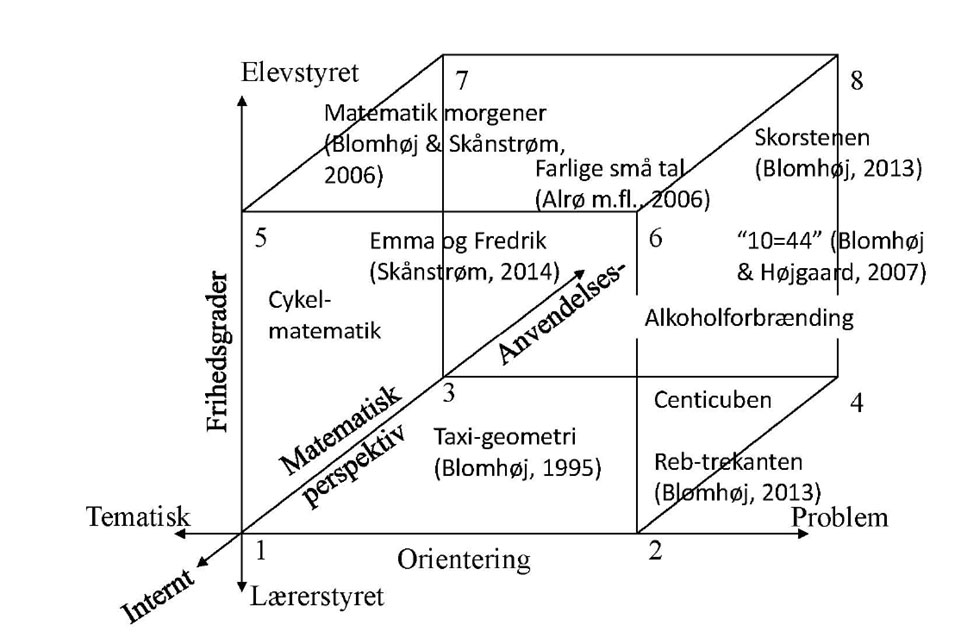
I bogen Fagdidaktik i matematik (2016) præsenterer Morten Blomhøj en model med tre dimensioner, og opfordrer matematiklærere til at anvende den i forbindelse med samarbejde omkring tilrettelæggelse af undersøgende forløb.
Forløbet om Cairoflisen i praksis
Cairoflisen er et eksempel på et undervisningsforløb, der har modelleringssituationen i fokus. I modellen med de tre dimensioner kan forløbet placeres et stykke op ad aksen med Frihedsgrader, mens forløbet i forhold til akserne med Matematisk perspektiv og Orientering mod problem kan placeres langt ude af de to akser.

Iscenesættelsen
Alle institutioner har et sted, der kan trænge til en ny belægning - det kan være et fælles område indenfor eller et større udendørs areal.
Iscenesættelsen er her det narrativ, opgaven sættes ind i:
”Skolen har fået et favorabelt tilbud på den specielle Cairo-flise, som blandt andet pryder gulvet i Industriens Hus på Rådhuspladsen i København.
Cairoflisen er en særlig femkantet flise, der kan tesselere.
Fire af de fem sider har samme længde.
I skal finde det sted her på skolen - inde eller ude, hvor I vil lægge cairofliser. I skal beslutte, hvilke mål, jeres fliser skal have. De fås nemlig i forskellige størrelser, men husk at de skal kunne bæres, og at granitten, der anvendes til flisen, har massefylden 2,5.”
Forslag til materialer:
Elevernes selvstændige og undersøgende arbejde
Elevernes undersøgende arbejde skal have tid til at folde sig ud. Der skal gives tid til at etablere et samarbejde i grupperne og eleverne bør kunne arbejde både ude og inde. Der skal være tid at etablere en både støttende og udfordrende dialog. For at dialogen ikke skal føles for tilfældig kan det anbefales at fokusere på hvilken feedback der gives til eleverne i løbet af deres arbejdsproces i de tre faser med udgangspunkt i stilladseringsmodellen fra ’Hvad kommer det an på?’
(Thomsen og Skånstrøm, 2017)
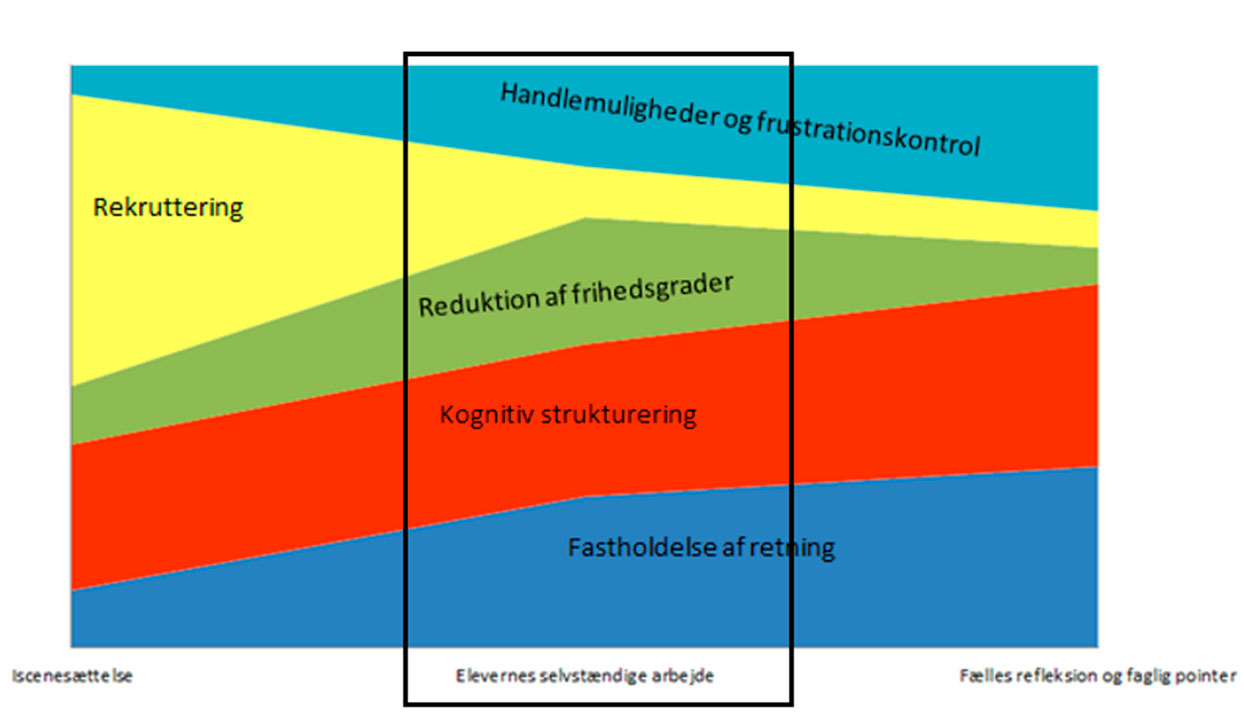
I denne fase arbejder eleverne selvstændigt det meste af tiden.
I tro på at rekrutteringen er foretaget - at eleverne er med på projektet med at lægge fliser - er det lærerens opgave at hjælpe dem med at fastholde deres valg og være med til at holde fokus på beslutninger, samtidig med der kan stilles faglige spørgsmål til de aktiviteter, som senere skal formidles i fællesskabet.
Fælles refleksion og faglige pointer
Resultaterne af elevernes anstrengelser skal fællesgøres. I tilfældet her med cairofliserne kan det gøres på forskellige måder. Eleverne kan tage fotos og/eller film, der viser udviklingen af processen med at beslutte størrelser på fliserne i forhold til, hvordan de kan dække det valgte område. Cairoflisernes form gør, at de ikke kan dække en rektangulær flade, så der kan tilføjes overvejelser omkring et ekstra forbrug og/eller en undersøgelse, om fliserne kan skæres, så de passer i de huller, der opstår i kanten af den valgte flade.
Andre måder at fællesgøre undersøgelsen på er fx at fremstille en brugsanvisning til en struktør eller brolægger, som har fået til opgave at lægge et gulv eller et område udenfor med cairofliserne. I dette arbejde, hvor resultatet skal både ses og bruges af mange mennesker, er kreativitet også en faktor i arbejdet med at lægge fliserne.
De faglige pointer er foruden tesseleringsaspektet koncentreret omkring begreberne areal, rumfang, massefylde og vægt.
I forhold til citaterne fra vejledningen har eleverne her arbejdet med en situation, der kunne være autentisk, hvor de har oversat problemstillingen til en model, som så har givet mulighed for at give en vurdering i forhold til virkeligheden.
Matematisk modellering har været den centrale matematiske kompetence, der har været i spil, men både tankegangs- og kommunikations-kompetencerne har været væsentlige at anvende i den totale løsning.
Eleverne har anvendt matematik til at løse den samlede problemstilling!
Lærerens rolle i denne afsluttende del af den åbne og undersøgende matematik kan opleves som noget frustrerende. Ikke alle elever når til det samme forslag, og de har heller ikke trådt den samme sti derhen. Men ved at benytte de nye spørgsmål, som åbner sig undervejs, kan vi som undervisere lede eleverne i individuelt tilpassede retninger, således at alle får passende faglige udfordringer. Vi kan og skal, når vi tager den fælles faglige refleksion mundtlig i klassen sørge for, at alle elever anerkendes for netop deres fremgangsmåde, samtidig med at de inspireres af deres klassekammeraters.
Ved på den måde at skabe respekt for hinandens tankeprocesser og arbejder, kan det jo være, at nogle elever tør arbejde i en helt ny retning næste gang!?
PS
Ifølge ’The Four Color Theorem’ er fire farver nok til, at ens farver ikke har en side til fælles i en tesselerende flade.
https://en.wikipedia.org/wiki/Four_color_theorem
Bilag til forløbet
Kreditering
Udarbejdet af Mikael Skånstrøm, Lektor, Via University College, Læreruddannelsen – Underviser i matematik.
Materialet tager udgangspunkt i en workshop på den virtuelle STEM-konference 2020.
Referencer
Alrø, H. og Johnsen-Høines, M. (2012): Trenger en å spørre for at være spørrende?. I: Alrø, H. & Johnsen-Høines, M.: Læringssamtalen i matematikkfagets praksis. Bok 1. Caspar Forlag.
Alrø, H,, Blomhøj, M., Bødtkjer, H., Skovsmose, O. og Skånstrøm, M.(2006): Farlige små tal - almendannelse i risikosamfundet.
Blomhøj, M. (2016): Fagdidaktik i matematik. Frydenlund.
Blomhøj, M. og Skånstrøm, M. (2006): Matematikmorgener - modellering i praksis. I: Blomhøj og Skovsmose, O.: Kunne det tænkes. Forlag Malling Beck.
Blomhøj, M. og Skånstrøm, M. (2016): Det kommer an på. I: Alrø, H. og Ragnes, T.E (red.): Matematikk for framtida, Caspar Forlag.
EUD matematik: Matematik: Fagbilag og vejledning, lokaliseret 16.11.20 på
Skovsmose, O. (1997): Kritisk matematikundervisning. I: Blomhøj, M. og Nissen, G. (red.): Hul i kulturen, Spektrum.
Thomsen, P.N. og Skånstrøm, M. (2017): Hvad kommer det an på. I: Henriksen, R.G. (red.): Feedback i matematik. Dafolo.
Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.


