Artikel
Højtbegavede børn og matematik
Hvordan adskiller højtbegavede børn sig fra andre børn, hvordan kan de identificeres og undervises, og hvad kan du som matematiklærer være opmærksom på?
Denne artikel oplister generelle kendetegn hos højtbegavede børn og kommer med bud på, hvordan matematikundervisningen kan tilrettelægges, så børnene undgår mistrivsel, fastholdes i en positiv læringsspiral og samtidig træner deres studiekompetencer.
Højtbegavede og talentfulde børn
Højtbegavede børn tilhører en lille gruppe af børn, som kognitivt ligger lige så langt fra middel, som børn med svære mentale handicaps. Disse børn går ofte i almindelige grundskoler uden særlig støtte og i omgivelser, der ikke altid kender til begavelsens udfordringer. I gennemsnit sidder der 1-2 højtbegavede elever i hver klasse. Tallet kan variere fra klasse til klasse, men ofte har mindst 2-3 elever i klassen brug for ekstra udfordringer. Både højtbegavede og talentfulde elever vil profitere af flere faglige udfordringer og nye måder at arbejde med opgaverne på. Så hvem er de højtbegavede børn, og hvordan kan læreren i den almindelige undervisning identificere, hvem der er højt begavet, og hvem der er talentfuld?
Talentfulde børn er, som alle andre grupper af børn, en kompleks gruppe med mange forskellige træk. De talentfulde børn kendetegnes blandt andet ved at have en skarp hjerne, og gennem systematisk træning og gode studievaner er de i stand til at præstere over det forventede niveau. I skolesammenhæng er der her tale om akademisk talent (jf. Ella Idsøe).
At være højt begavet er derimod en iboende evne, der gør, at barnet tænker, sanser og føler anderledes end andre. Et højtbegavet barn behøver ikke nødvendigvis samme antal gentagelser og træning som resten af klassen for at opnå resultater over klassens niveau. Deres særlige videbegærlighed, nysgerrighed, gode hukommelse, store drive og logiske ræsonnementer gør, at det faglige indhold potentielt kan læres hurtigt og bruges i andre sammenhænge.
Identifikation
Det er som regel skolepsykologen, som tester barnets IQ med en WISC-test, der viser, hvor barnet kognitivt er placeret, styrkeområder og eventuelle udfordringer. Ofte er det dog først, når barnet mistrives, eller hvis der er mistanke om diagnose, at der sættes gang i test.
Læreren kan selv komme langt i arbejdet med at identificere højt begavede børn. Ved at anvende særlige tjeklister og screeningsværktøjer kan læreren få en god indikation af hvem, der er højt begavet eller ligger i området omkring. Tjeklisterne kommer ikke med et samlet tal for barnets IQ, men arbejder med en cut-off score. En grundig identifikation af de højtbegavede børn i klassen kræver både kvalitative data med observation og interview, samt kvantitative tjeklister og resultater fra test og prøver. Når begge former for data inddrages i identifikationsprocessen, minimeres risikoen for at overse barnets begavelse og misforstå adfærden, som kan være så anderledes, at der ofte tænkes i diagnoser.
Når et klasseteam arbejder med identifikationsprocessen, kan dialogen bidrage til at nuancere oplevelserne af børnenes styrker og udfordringer. En elev, som nogle opfatter som normal- eller måske ubegavet, kan af en anden lærer opfattes højt begavet. Læringsbetingelser, gruppen, interesser og relationen mellem lærer og elev har stor betydning for, hvordan eleven fremstår.
Et højtbegavet barn scorer ikke nødvendigvis højt i alle test og prøver og ej heller i alle fag. De har ofte brug for at indsamle og bearbejde en stor mængde data, inden de afgiver et sikkert, velovervejet og konsekvensgennemtænkt svar. De kan derfor have behov for mere tid og dermed fremstå langsomme og usikre.
Find en liste med 20 kendetegn på højtbegavede elever i PDF’en nederst på siden.
Trivsel og mistrivsel
Højtbegavede børns adfærd kan på nogle punkter minde om adfærden hos børn med ADHD og Aspergers Syndrom. Et højtbegavet barn med et stort drive, højt energiniveau, uro i kroppen, store følelsesmæssige udsving, ringe koncentration og i klassesammenhæng sociale udfordringer kan forveksles med et barn med ADHD. Og et højtbegavet introvert barn, der har særinteresser, er gammelklog, som har en ekstrem god hukommelse, er distræt, virker nørdet og har få venner i klassen kan forveksles med et barn med Aspergers Syndrom. Andre læringsudfordringer, der slører billedet af en høj begavelse, kan være dysleksi og talblindhed.
Da mange lærere ikke ved så meget om kendetegn på høj begavelse, kan højtbegavede børn forveksles med børn med læringsudfordringer. Derfor må læreren være nysgerrig på, hvad barnet kan og ikke kan i gunstige og optimale læringssituationer - og have fokus på potentialet frem for udfordringerne.
Højtbegavede børn føler sig ofte anderledes eller forkerte. De lærer tingene i første eller andet forsøg og kan derfor mangler faglige og anderledes udfordringer. De har ingen eller få at dele deres interesser og viden med, og derfor er de i særlig risiko for at udvikle mistrivsel og underydelse (jf. S. Bisgaard).
|
Kendetegn ved højtbegavede børn i trivsel |
Kendetegn ved højtbegavede børn i mistrivsel |
|
Lærer hurtigt nyt stof |
Giver op efter 1. forsøg, underyder ved rutine- og repetitionsopgaver, er ligeglade |
|
Har en udviklet form for humor |
Er ironiske eller sarkastiske |
|
Er ivrige, opvakte og har et højt energiniveau |
Er rastløse, har svært ved at sidde stille, forstyrrer andre. |
|
Arbejder målrettet og dedikeret |
Er stædige og ufleksible |
|
Er sensitive, følsomme og modtagelige |
Har et skrøbeligt ego, er ekstremt følsomme for kritik |
Høj begavelse og matematik
En del højtbegavede børn holder allerede i en tidlig alder af mønstre, gåder, grublere, problemløsning, tal og naturvidenskab. De kan lægge svære puslespil og genkende og huske bilmærker og nummerplader. Nogle af dem lærer sig selv at regne, inden de begynder i skole, og mens andre arbejder med tal fra 1-10, kan de højtbegavede børn måske allerede tabeller. De kan håndtere store mængder tal og løse opgaver med langt større kompleksitet end deres jævnaldrende klassekammerater, og de har øje for detaljer og spotter hurtigt fejl og unøjagtigheder.
De højtbegavede børns evne til intuitivt og hurtigt at se løsninger gør, at mellemregninger, og i deres øjne andre unødvendigheder, springes over. De bliver ”dovne”, hvilket på sigt kan være en udfordring. Mellemregninger er ikke kun vigtige for at komme frem til resultatet, de viser også, hvilke overvejelser eleven har gjort sig og deres matematiske tænkning. Det må derfor forventes, at eleven demonstrerer færdighederne heri, inden der arbejdes videre med nyt.
For at udfordre højtbegavede børn bedst muligt, må opgaverne ofte være så komplekse, at gætteri ikke hver gang er en mulighed. De skal trænes i at arbejde sig frem til en løsning og inddrage relevante beregninger, formler og overvejelser. Gentagelser og repetition er sjældent nødvendigt, men at skabe ny forståelse og nye sammenhænge ud fra eksisterende viden er med til at gøre undervisning spændende og relevant.
Kendetegn på højtbegavede børn i matematik kan være, at de:
- lærer nemt og hurtigt.
- har en abstrakt tænkning og kreative løsningsforslag.
- er problemløsende og logisk tænkende.
- kan se et resultat uden at kunne forklare, hvordan det er fremkommet.
- er gode til mønstre og grublere og kan lide at nørde med formler og beviser.
- stiller spørgsmål, der udfordrer viden og måden at løse opgaver på.
- er gode til matematiske programmer og systemer og håndtere store mængder tal.
- kan løse opgaver til højere klassetrin og scorer højt i matematiske test og prøver.
Iflølge Francoys Gagne vil højtbegavede børn have evnerne til at være i top 10 i alle fag. Så når højtbegavede børn kommer i vanskeligheder i matematik, er der sandsynlighed for, at det skyldes manglende interesse, kedsomhed, måden der undervises på eller relationen til læreren fremfor manglende evner.
Undgå mistrivsel i matematik
For at undgå, at højtbegavede børn keder sig og mistrives i matematik, kan disse forhold indtænkes i undervisningen i både matematik og i andre fag:
- Anerkend potentialet og inddrag familien i samarbejdet både i forhold til identifikation, og måden barnet tænker matematik.
- Vær tydelig omkring formål og mål med skriftlige afleveringer.
- Støt i forhold til udfordringerne (struktur, gruppearbejde, kommunikation, mellemregninger og træning).
- Vær opmærksom på barnets rolle i gruppearbejde – hvad er formålet og målet?
- Stilladser opgaver meget tydeligt og vær omhyggelig med opgavebeskrivelser og sprog.
- Undgå, at barnet deltager i gentagne rutineopgaver og repetition – hav alternativer parat.
- Afstem med meningsfyldte lektier og giv alternative grublere – træn det svære.
- Lad barnet arbejde med anderledes og selvstændige fordybelsesopgaver.
- Undgå at bruge barnet som hjælpelærer – brug kun barnet som ekspert i særlige situationer!
Differentieret matematikundervisning
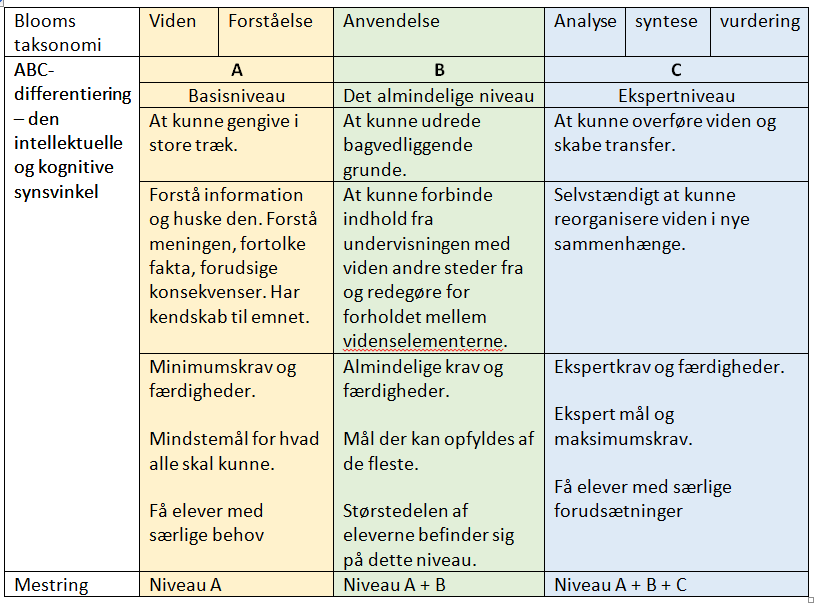
Højtbegavede elever har som alle andre brug for at blive udfordret ud fra deres kognitive potentiale. De overses ofte, fordi læreren vurderer, at de kan klare sig selv, men et højtbegavet barn har også brug for udfordringer, der kræver vejledning og støtte. En måde at differentiere undervisningen på, så der også bliver udfordringer for de højtbegavede børn, kunne være med Kirsten Baltzer og Poul Nissens ABC-differentiering. Udgangspunktet er her at anerkende elevernes forskellige mestringsniveauer.
ABC-differentiering arbejder med en planlægningsramme, hvor alle elever arbejder med det samme emne/stofområde, men på tre forskellige niveauer A, B og C. Eleverne er ikke bundet til et niveau. Da størstedelen af klassen bør arbejde med opgaver på B niveau, vil der kun være få elever, i hver sin ende af det kognitive spektrum, der arbejder på de to andre. Når læreren planlægger sin matematikundervisning ud fra ABC-princippet, er der et fælles læringsmål for undervisningen, eksempelvis geometri, og tre individuelle mestringsniveauer.
ABC-differentiering arbejder jf. læseplanen i matematik med et fælles udgangspunkt, som rummer mulighed for flere forskellige tilgange, strategier og metoder, så som den åbne og undersøgende opgave.
- A-opgaver, basisniveau: For elever, der har brug for en del gentagelser, før stoffet mestres. Lægger sig tæt op ad det, læreren netop har undervist i.
- B-opgaver, det almindelige niveau: Udfærdiges, så langt størstedelen af eleverne i klassen udfordres. Bygger videre på A-niveauets ”at huske og forstå” og arbejder videre med ”at anvende og analysere”. B-opgaver indeholder mål for, hvad der forventes, at eleverne skal kunne på pågældende klassetrin.
- C-opgaver, ekspertniveau: For få elever i klassen. Bygger videre på A- og B-opgavernes mestringsniveau, og vil være de opgaver, som højtbegavede børn i trivsel ofte vil skulle udfordres med. Hvis størstedelen af klassen er i stand til at løse C-opgaverne, er de som udgangspunkt for lette, og udfordrer derfor ikke højtbegavede børn i tilstrækkelig grad.
Når et nyt stofområde introduceres, vil en stor gruppe elever befinde sig på A-niveau, som i forhold til Blooms taksonomi handler om ”at huske og forstå”. De højtbegavede vil dog hurtigt have behov for udfordringer over A-niveau. ABC-opgaver udvikler sig i takt med, at det lærte akkumuleres.
ABC-differentieringsmodellen er dynamisk, tilpasses elevernes læringsprogression og sikrer, at alle elever skal stå en lille smule på tæer. Både dem på A-niveau, B-niveau og C-niveau.
Matematikvejlederens rolle
At skabe et inkluderende læringsmiljø kræver, at læreren har den nødvendige viden om elevernes forudsætninger og viden om, hvordan undervisningen kan tilrettelægges, så alle får de udfordringer og den støtte, de har brug for. For at understøtte dette kan matematikvejlederens viden om matematik kombineres med specialpædagogisk viden om højtbegavede børns styrker og udfordringer.
Lektor og ph.d Lotte Hedegaard Sørensen beskriver en væsentlig forskel mellem special- og almenpædagogik. I specialpædagogikken tages der afsæt i børnenes individuelle situationer, og undervisningen tilrettelægges ud fra det. I almenpædagogikken er der i langt højere grad fokus på undervisningen i fag og på hele klasser. Med specialpædagogisk viden om højtbegavede børn vil matematikvejlederen sammen med klassens lærer kunne reflektere fagligt og løbende justere indsatsen. Det vil også være muligt for vejlederen at indsamle viden om indsatser og undervisning på tværs af klasser og årgange, så der kan opbygges fælles viden og forståelse for højtbegavede børns unikke og til tider udsatte læringssituationer.
En rapport fra Eva (Danmarks Evalueringsinstitut) konkluderer netop, at de inkluderende fællesskaber fungerer bedst, når lærere og vejledere, eventuelt med specialpædagogisk viden, arbejder sammen i klassen.
Kreditering
Artiklen er udarbejdet af Rikke Christensen, lærer, konsulent og indehaver af firmaet Clever Consulting – fokus på højtbegavede børn.
Baltzer, Kyed & Nissen (2014). Dygtig, dygtigere, dygtigst. Frederikshavn: Dafolo.
Branca Lie (2016). Højt begavede børn i børnehavealderen. København: Dansk Psykologisk Forlag A/S.
Det nationale Forsknings- og Analysecenter for Velfærd (2015). Indsatser målrettet højt begavede børns faglige udvikling og trivsel. København: VIVE.
Ella Idsøe (2014). Elever med akademisk talent i skolen. Oslo: Cappelen Damm Akademisk.
Kortnum, Nielsen, Videsen (2016). Mindsetbaseret undervisning. København: Dansk Psykologisk forlag.
Linda Kreger Silverman, Gifted Development Center.
Ole Kyed (2015). De intelligente børn. København: Akademisk Forlag.
UVM (2011). Talentudvikling – Evaluering og strategi. Talentrapport. København: UVM.
Tekstindholdet på denne side må bruges under følgende Creative Commons-licens - CC/BY/NC/SA Kreditering/Ikke kommerciel/Deling på samme vilkår. Creative Commons-licensen gælder kun for denne side, ikke for sider, der måtte henvises til fra denne side.
Billeder, videoer, podcasts og andre medier og filer på siden er underlagt almindelig ophavsret og kan ikke anvendes under samme Creative Commons-licens som sidens tekstindhold.